题目内容
【题目】如图所示,直线y=x与y轴之间有垂直于xOy平面向外的匀强磁场B1,直线x=d与y=x间有沿y轴负方向的匀强电场,电场强度E=1.0×104V/m,另有一半径R=1.0m的圆形匀强磁场区域,磁感应强度B2=0.20T,方向垂直坐标平面向外,该圆与 直线x=d和x轴均相切,且与x轴相切于S点。一带负电的粒子从S点沿y轴的正方向以速度v0进人圆形磁场区域,经过一段时间进入磁场区域B1,且第一次进入磁场B1时的速度方向与直线y=x垂直。粒子速度大小v0=1.0×105m/s,粒子的比荷为q/m= 5.0×105C/kg,粒子重力不计。求:
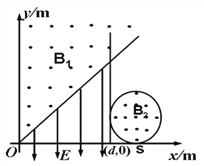
(1)坐标d的值;
(2)要使粒子无法运动到x轴的负半轴,则磁感应强度B1应满足的条件;
(3)在(2)问的基础上,粒子从开始进入圆形磁场至第二次到达直线y=x上的最长时间。(第(3)问结果保留两位有效数字,π=3.14)
【答案】(1)4m
(2)0<B1≤0.10T或B1≥0.24T
(3)![]()
【解析】试题分析:(1)由带电粒子在匀强磁场B2中运动可得:![]()
解得:r = 1m=R
粒子进入匀强电场以后,做类平拋运动,设水平方向的位移为x1,竖直方向的位移为y1
水平方向![]()
竖直方向![]()
其中![]()
联立解得: x1 = 2m,y1= 1m
由图示几何关系得:![]()
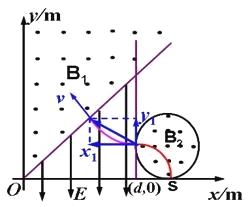
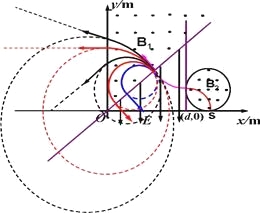
(2)可使粒子无法运动到x负半轴
①设当匀强磁场磁感应强度为B3时,粒子从电场垂直边界进入匀强磁场后,轨迹与y轴相切,此时粒子在磁场中运动半径为r1,由如图所示几何关系得:
![]()
解得:![]()
由牛顿第二定律得:![]()
解得:![]()
②设当匀强磁场磁感应强度为B4时,粒子垂直打在y轴上,粒子在磁场中运动半径为r2,由如图所示几何关系得:![]()
由牛顿第二定律得:![]()
解得: B4==0.10T
综上所述,要使粒子无法运动到x轴的负半轴,则磁感应强度B1应满足的条件是:0<B1≤0.10T或B1≥0.24T
(3)设粒子在B2中运动时间为t1;在电场中运动时间为t2;在磁场B1中运动,当轨迹与y轴相切时所用的时间最长为t3
所以有![]() ,
,![]() ,
,![]()
则当粒子从开始进入圆形磁场至第二次到达直线y=x上所用的最长时间为t
![]()