题目内容
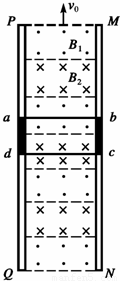
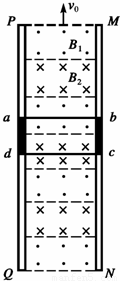
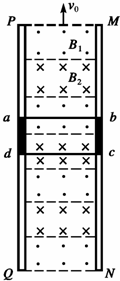 德国亚琛工业大学的科研人员成功开发了一种更先进的磁动力电梯升降机,满足上千米摩天大楼中电梯升降的要求.如图所示就是一种磁动力电梯的模拟图,在竖直平面上有两根很长的平行竖直轨道,轨道间有垂直于轨道平面的匀强磁场B1和B2,B1和B2的大小相等,方向相反,两磁场始终竖直向上作匀速运动.电梯轿厢固定在如图所示的金属框abcd内(电梯轿厢在图中未画出),并且与之绝缘,利用磁场与金属框间的相互作用,使电梯轿厢获得动力.已知电梯载人时的总质量为5.0×103kg,金属框垂直轨道的边长Lcd=2.5m,两磁场的宽度均与金属框的边长Lad相同,金属框整个回路的电阻R=1.0×10-3Ω,磁场的磁感应强度B1=B2=1T,不计轨道及空气阻力,g取10m/s2.求:
德国亚琛工业大学的科研人员成功开发了一种更先进的磁动力电梯升降机,满足上千米摩天大楼中电梯升降的要求.如图所示就是一种磁动力电梯的模拟图,在竖直平面上有两根很长的平行竖直轨道,轨道间有垂直于轨道平面的匀强磁场B1和B2,B1和B2的大小相等,方向相反,两磁场始终竖直向上作匀速运动.电梯轿厢固定在如图所示的金属框abcd内(电梯轿厢在图中未画出),并且与之绝缘,利用磁场与金属框间的相互作用,使电梯轿厢获得动力.已知电梯载人时的总质量为5.0×103kg,金属框垂直轨道的边长Lcd=2.5m,两磁场的宽度均与金属框的边长Lad相同,金属框整个回路的电阻R=1.0×10-3Ω,磁场的磁感应强度B1=B2=1T,不计轨道及空气阻力,g取10m/s2.求:(1)当电梯以某一速度匀速上升时,金属框中的感应电流的大小及图示时刻感应电流的方向.
(2)假设设计要求电梯以v1=10m/s的速度向上匀速运动,则磁场向上运动速度v应该为多大?
(3)在电梯以v1=10m/s的速度向上作匀速运动时,为维持它的运动,磁场每秒需提供的总能量.
分析:(1)电梯上升的动力是ab、cd所受的安培力的合力.匀速运动时,由平衡条件和安培力可求出感应电流的大小,由右手定则判断方向.
(2)电梯以v1=10m/s的速度向上匀速运动,磁场向上运动速度v,电梯相对于磁场的速度大小为v-v1,由欧姆定律和感应电动势可求出v.
(3)根据能量转化和守恒定律求得磁场每秒需提供的总能量.
(2)电梯以v1=10m/s的速度向上匀速运动,磁场向上运动速度v,电梯相对于磁场的速度大小为v-v1,由欧姆定律和感应电动势可求出v.
(3)根据能量转化和守恒定律求得磁场每秒需提供的总能量.
解答:解:设匀强磁场B1=B2=B
(1)金属框匀速运动,则金属框受到的安培力与重力平衡.得到
2BILcd=mg
解得 I=1×104A
由右手定则判断出感应电流方向为逆时针方向.
(2)金属框中感应电动势E=2BLcd(v-v1)
则得I=
代入解得 v=12m/s
(3)金属框中的焦耳热功率P1=I2R,重力的功率P2=mgv1
由能量守恒得,磁场每秒提供的能量W=(P1+P2)t=6×105J
答:(1)金属框中的感应电流的大小为1×104A,感应电流的方向为逆时针方向.
(2)磁场向上运动速度v应该为12m/s.
(3)为维持电梯的运动,磁场每秒需提供的总能量为6×105J.
(1)金属框匀速运动,则金属框受到的安培力与重力平衡.得到
2BILcd=mg
解得 I=1×104A
由右手定则判断出感应电流方向为逆时针方向.
(2)金属框中感应电动势E=2BLcd(v-v1)
则得I=
| E |
| R |
代入解得 v=12m/s
(3)金属框中的焦耳热功率P1=I2R,重力的功率P2=mgv1
由能量守恒得,磁场每秒提供的能量W=(P1+P2)t=6×105J
答:(1)金属框中的感应电流的大小为1×104A,感应电流的方向为逆时针方向.
(2)磁场向上运动速度v应该为12m/s.
(3)为维持电梯的运动,磁场每秒需提供的总能量为6×105J.
点评:本题理论联系实际问题,与常规题不同的是,金属框ab、cd都切割磁感线,产生两个感应电动势,两个边都受安培力,而且磁场与导体一起运动,有效的切割速度是两者的相对速度.

练习册系列答案
相关题目
 (2013?浙江模拟)近年来,越来越高的摩天大厦在世界各地落成.日本东京的千年塔设计170层、840米高,而由西班牙著名建筑设计大师哈韦尔皮奥斯设计的上海“超群大厦”甚至将高达1249.9米.然而,至今普遍使用的钢索吊挂式电梯已经不再适台这样的高度,因为需要的钢索太长、太重会因承受不了自身的重量而断裂.为此德国亚琛工业大学的科研人员设计出了一种磁动力电梯,其原理是利用移动的磁场来带动电梯向上或向下运动.工作原理可简化如下:如图所示,PQ和MN是两根平行竖直轨道,轨道间有垂直轨道平面的等大反向匀强磁场B1和B2,B1=B2=1T,两磁场可向上作匀速运动.电梯轿厢固定在金属框abcd内(轿厢未画出).现己知电梯载人时的总质量为m=1.0×104kg,运动时所受阻力f=1000N,金属框垂直轨道的边长Lcd=2m,两磁场的宽度均与金属框的边长Lac相同,金属框的总电阻为R=1.0×10-3Ω,某时段磁场以v0=10m/s的速度向上匀速运动,g=10m/s2求:
(2013?浙江模拟)近年来,越来越高的摩天大厦在世界各地落成.日本东京的千年塔设计170层、840米高,而由西班牙著名建筑设计大师哈韦尔皮奥斯设计的上海“超群大厦”甚至将高达1249.9米.然而,至今普遍使用的钢索吊挂式电梯已经不再适台这样的高度,因为需要的钢索太长、太重会因承受不了自身的重量而断裂.为此德国亚琛工业大学的科研人员设计出了一种磁动力电梯,其原理是利用移动的磁场来带动电梯向上或向下运动.工作原理可简化如下:如图所示,PQ和MN是两根平行竖直轨道,轨道间有垂直轨道平面的等大反向匀强磁场B1和B2,B1=B2=1T,两磁场可向上作匀速运动.电梯轿厢固定在金属框abcd内(轿厢未画出).现己知电梯载人时的总质量为m=1.0×104kg,运动时所受阻力f=1000N,金属框垂直轨道的边长Lcd=2m,两磁场的宽度均与金属框的边长Lac相同,金属框的总电阻为R=1.0×10-3Ω,某时段磁场以v0=10m/s的速度向上匀速运动,g=10m/s2求: