题目内容
【题目】一轻质橡皮筋原长L=50cm,劲度系数k=100N/m,将其上端固定在天花板上O点,如图甲所示.
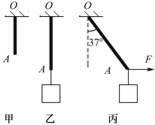
(1)在其下端A处用细线悬挂重为16N的物块,静止后如图乙所示,求橡皮筋的伸长量x1;
(2)在图乙中A处用一水平外力向右缓慢拉动,使橡皮筋与竖直方向成37°角时保持静止,如图丙所示,求橡皮筋的伸长量x2和物块高度的变化量h.(sin37°=0.6,cos37°=0.8)
【答案】(1)橡皮筋的伸长量为0.16m;
(2)橡皮筋的伸长量为0.2m,物块高度的变化量h为0.1m.
【解析】
试题分析:(1)根据题意木块处于平衡状态,F1=G,由胡克定律列式即可求解;
(2)橡皮筋与竖直方向成37°角时保持静止,受力分析,根据平衡条件列式,再根据胡克定律结合几何关系求解.
解:(1)根据题意木块处于平衡状态,F1=G
由胡克定律得F1=kx1
则![]() m
m
(2)橡皮筋与竖直方向成37°角时保持静止,受力分析,可得
![]()
解得:F2=20N
根据胡克定律F2=kx2
得![]() =0.2 m
=0.2 m
乙图中A点到O点的高度h1=L+x1=0.66m
丙图中A点到O点的高度h2=(L+x2)cos37°=0.56m
则重物上升的高度等于A点上升的高度,h=h1﹣h2=0.1m
答:(1)橡皮筋的伸长量为0.16m;
(2)橡皮筋的伸长量为0.2m,物块高度的变化量h为0.1m.

练习册系列答案
相关题目