题目内容
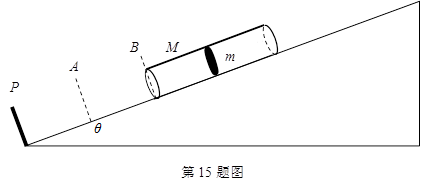
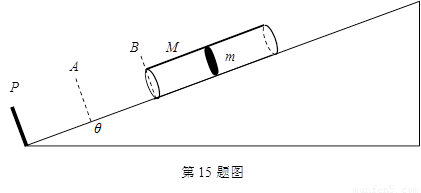
(16分)光滑的斜面倾角θ=30º,斜面底端有弹性挡板P,长2l、质量为M的两端开口的圆筒置与斜面上,下端在B点处, PB=2l,圆筒的中点处有一质量为m的活塞,M=m.活塞与圆筒壁紧密接触,最大静摩擦力与滑动摩擦力相等为f=mg/2.每当圆筒中的活塞运动到斜面上AB区间时总受到一个沿斜面向上F=mg的恒力作用,AB=l.现由静止开始从B点处释放圆筒.
(1)求活塞位于AB区间之上和进入AB区间内时活塞的加速度大小;
(2)求圆筒第一次与挡板P碰撞前的速度和经历的时间;
(3)圆筒第一次与挡板P瞬间碰撞后以原速度大小返回,求圆筒沿斜面上升到最高点的时间.
(1)a2=0;(2)3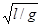 ;(3)
;(3)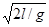
【解析】(16分)考查牛顿第二定律的综合应用,多物体、多过程问题的受力分析和过程分析.
(1)活塞在AB之上时,活塞与筒共同下滑加速度 a1=gsin300 (1分)
活塞在AB区间内时,假设活塞与筒共同下滑,(M+m)gsin300-F=(M+m)a
解得:a=0
对m:受向上恒力F=mg, 此时F-mg sin300-f=0 f刚好等于mg/2,假设成立.(1分)
活塞的加速度a2=0 (1分)
(2)圆筒下端运动至A活塞刚好到达B点 此时速度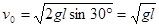 (1分)
(1分)
经历时间t1, l=gsin30º t12/2
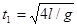 (1分)
(1分)
接着m向下匀速.
M 受力 f-Mg sin300=mg/2-mg/2=0 (1分)
所以m 和M都以v0作匀速运动,到达P时速度即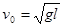 (1分)
(1分)
匀速运动时间t2=l/ v0=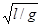 (1分)
(1分)
总时间t=3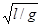 (1分)
(1分)
(3)M反弹时刻以v0上升,m过A点以v0下滑,以后由于摩擦力和重力,m在M内仍然做匀速下滑,M以加速度a‘=(Mgsin300+f)/M=g减速, (1分)
m离开M时间t1为 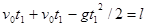 (1分)
(1分)
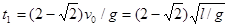 (1分)
(1分)
此时M速度v=v0-gt1=
(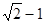 )v0,
(1分)
)v0,
(1分)
接着M以加速度a/=g/2向上减速,t2=v/a/=2v/g=2(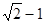 )
)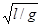 (1分)
(1分)
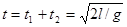 (2分)
(2分)

 一本好题口算题卡系列答案
一本好题口算题卡系列答案 如图所示,一个重为200N的物体,放在倾角为20°的粗糙斜面上保持静止.已知物体与斜面间的动摩擦因数为0.4.求:(附:你可能需要用到的数据sin20°=0.34 cos20°=0.94 tan20°=0.36 g=10m/s2)
如图所示,一个重为200N的物体,放在倾角为20°的粗糙斜面上保持静止.已知物体与斜面间的动摩擦因数为0.4.求:(附:你可能需要用到的数据sin20°=0.34 cos20°=0.94 tan20°=0.36 g=10m/s2)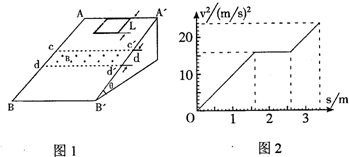 一个质量m=0.1kg的正方形金属框总电阻R=0.5Ω,金属框放在表面是绝缘且光滑的斜面顶端,自静止开始沿斜面下滑,下滑过程中穿过一段边界与斜面底边BB′平行、宽度为d的匀强磁场后滑至斜面底端BB′,设金属框在下滑时即时速度为v,与此对应的位移为s,那么v2-s图象如图2所示,已知匀强磁场方向垂直斜面向上.试问:
一个质量m=0.1kg的正方形金属框总电阻R=0.5Ω,金属框放在表面是绝缘且光滑的斜面顶端,自静止开始沿斜面下滑,下滑过程中穿过一段边界与斜面底边BB′平行、宽度为d的匀强磁场后滑至斜面底端BB′,设金属框在下滑时即时速度为v,与此对应的位移为s,那么v2-s图象如图2所示,已知匀强磁场方向垂直斜面向上.试问: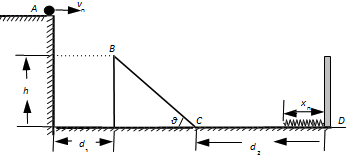 如图所示,质量为 m=0.1kg的小球置于平台末端A点,平台的右下方有一个表面光滑的斜面体,在斜面体的右边固定一竖直挡板,轻质弹簧拴接在挡板上,弹簧的自然长度为 x0=0.3m,斜面体底端 C 距挡板的水平距离为 d2=1m,斜面体的倾角为 θ=45°,斜面体的高度 h=0.5m.现给小球一大小为 v0=2m/s的初速度,使之在空中运动一段时间后,恰好从斜面体的顶端 B 无碰撞地进入斜面,并沿斜面运动,经过 C 点后再沿粗糙水平面运动,过一段时间开始压缩轻质弹簧.小球速度减为零时,弹簧被压缩了△x=0.1m.已知小球与水平面间的动摩擦因数 μ=0.5,设小球经过 C 点时无能量损失,重力加速度 g=10m/s2,求:
如图所示,质量为 m=0.1kg的小球置于平台末端A点,平台的右下方有一个表面光滑的斜面体,在斜面体的右边固定一竖直挡板,轻质弹簧拴接在挡板上,弹簧的自然长度为 x0=0.3m,斜面体底端 C 距挡板的水平距离为 d2=1m,斜面体的倾角为 θ=45°,斜面体的高度 h=0.5m.现给小球一大小为 v0=2m/s的初速度,使之在空中运动一段时间后,恰好从斜面体的顶端 B 无碰撞地进入斜面,并沿斜面运动,经过 C 点后再沿粗糙水平面运动,过一段时间开始压缩轻质弹簧.小球速度减为零时,弹簧被压缩了△x=0.1m.已知小球与水平面间的动摩擦因数 μ=0.5,设小球经过 C 点时无能量损失,重力加速度 g=10m/s2,求: