题目内容
18. 如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区的右边界.现有一质量为m.电量为-q的带电粒子,从电场中的P点以初速度v0沿x轴正方向开始运动,已知P点的坐标为(-L,0)且L=$\frac{m{{v}_{0}}^{2}}{qE}$,试求:
如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区的右边界.现有一质量为m.电量为-q的带电粒子,从电场中的P点以初速度v0沿x轴正方向开始运动,已知P点的坐标为(-L,0)且L=$\frac{m{{v}_{0}}^{2}}{qE}$,试求:(1)带电粒子运动到Y轴上时的速度
(2)要使带电粒子能穿越磁场区域而不再返回到电场中,磁场的宽度最大为多少(不计重力)
分析 (1)粒子在电场中受到的电场力的方向向上,粒子做的事类平抛运动,水平方向做的是匀速运动,竖直方向做的是匀加速直线运动,从而可以求得带电粒子运动到Y轴上时的速度;
(2)当磁场的运动的轨迹恰好与磁场的有边沿相切时,此时的磁场的宽度最大,根据粒子的运动的轨迹可以求得磁场的宽度最大值.
解答 解:(1)带电粒子在电场中做类平抛运动,设粒子进入磁场时的速度大小为v,
速度方向与y轴的夹角为θ,如图所示,则:
水平方向:L=v0t,
竖直方向:vy=at=$\frac{qE}{m}$t,
速度:v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{2}$v0,
cosθ=$\frac{{v}_{y}}{{v}_{\;}}$=$\frac{\sqrt{2}}{2}$,θ=45°;
(2)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{R}$,解得:R=$\frac{mv}{qB}$,
要使带电粒子能穿越磁场区域,磁场的宽度应满足的条件为:d≤(1+cosθ)R
即:d≤$\frac{(1+\sqrt{2})m{v}_{0}}{qB}$;
答:(1)带电粒子运动到Y轴上时的速度大小为$\sqrt{2}$v0,方向与y轴成45°角;
(2)要使带电粒子能穿越磁场区域而不再返回到电场中,磁场的宽度最大为:$\frac{(1+\sqrt{2})m{v}_{0}}{qB}$.
点评 本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.在电磁波发射技术中,使电磁波随各种信号而改变的技术叫调制,调制分调幅和调频两种.如图①所示有A、B两幅图.在收音机电路中天线接收下来的电信号既有高频成分又有低频成分,经放大后送到下一级,需要把高频成分和低频成分分开,只让低频成分输入下一级,如果采用如练图②所示的电路,图中虚线框a和b内只用一个电容器或电感器.以下关于电磁波的发射和接收的说法中,正确的是( )


| A. | 在电磁波的发射技术中,图①中A是调幅波 | |
| B. | 在电磁波的发射技术中,图①中B是调幅波 | |
| C. | 图②中a是电容器,用来通高频阻低频,b是电感器,用来阻高频通低频 | |
| D. | 图②中a是电感器,用来阻交流通直流,b是电容器,用来阻高频通低频 |
7. 如图,质量为M、长度为L的小车静止在光滑的水平面上.质量为m的小物块放在小车的最左端.现在一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动,物块和小车之间的摩擦力为f.经过时间t,小车运动的位移为s,物块刚好滑到小车的最右端.( )
如图,质量为M、长度为L的小车静止在光滑的水平面上.质量为m的小物块放在小车的最左端.现在一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动,物块和小车之间的摩擦力为f.经过时间t,小车运动的位移为s,物块刚好滑到小车的最右端.( )
 如图,质量为M、长度为L的小车静止在光滑的水平面上.质量为m的小物块放在小车的最左端.现在一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动,物块和小车之间的摩擦力为f.经过时间t,小车运动的位移为s,物块刚好滑到小车的最右端.( )
如图,质量为M、长度为L的小车静止在光滑的水平面上.质量为m的小物块放在小车的最左端.现在一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动,物块和小车之间的摩擦力为f.经过时间t,小车运动的位移为s,物块刚好滑到小车的最右端.( )| A. | 此时物块的动能为(F-f)(s+L) | |
| B. | 这一过程中,物块对小车所做的功为f(s+L) | |
| C. | 这一过程中,物块和小车增加的机械能为F(s+L)-fL | |
| D. | 这一过程中,物块和小车产生的内能为f(s+L) |
8.(多选)假设一小型宇宙飞船沿人造地球卫星的轨道在高空做匀速圆周运动,运动周期为T,如果飞船沿与其速度相反的方向发射一个物体A(假设物体的速度可以从较小值到足够大值的任意取值),之后它们的运动可能是( )
| A. | 物体A的运动周期小于T,飞船不可能在原轨道上运动T | |
| B. | 物体A的运动周期等于T,飞船的运动周期大于T | |
| C. | 物体A竖直下落,飞船在原轨道上运动 | |
| D. | 物体A和飞船的运动周期都大于T |


 用圆弧状玻璃砖做测定玻璃折射率的实验时,先在白纸上放好圆弧状玻璃砖,在玻璃砖的一侧竖直插上两枚大头针P1、P2;然后在玻璃砖的另一侧观察,调整视线使P1的像被P2挡住,接着在眼睛所在的一侧插两枚大头针P3和P4,使P3挡住P1和P2的像,P4挡住P3和P1、P2的像,在纸上标出大头针位置和圆弧状玻璃砖轮廓如图所示(E为两圆弧圆心;图中已画出经P1、P2点的入射光线).
用圆弧状玻璃砖做测定玻璃折射率的实验时,先在白纸上放好圆弧状玻璃砖,在玻璃砖的一侧竖直插上两枚大头针P1、P2;然后在玻璃砖的另一侧观察,调整视线使P1的像被P2挡住,接着在眼睛所在的一侧插两枚大头针P3和P4,使P3挡住P1和P2的像,P4挡住P3和P1、P2的像,在纸上标出大头针位置和圆弧状玻璃砖轮廓如图所示(E为两圆弧圆心;图中已画出经P1、P2点的入射光线).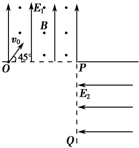 如图所示,竖直平面内有相互垂直的匀强电场和匀强磁场,电场强度E1=2500N/C,方向竖直向上;磁感应强度B=103T.方向垂直纸面向外;有一质量m=1×10-2kg、电荷量q=4×10-5C的带正电小球自O点沿与水平线成45°角以v0=4m/s的速度射入复合场中,之后小球恰好从P点进入电场强度E2=2 500N/C,方向水平向左的第二个匀强电场中.不计空气阻力,g取10m/s2.求:
如图所示,竖直平面内有相互垂直的匀强电场和匀强磁场,电场强度E1=2500N/C,方向竖直向上;磁感应强度B=103T.方向垂直纸面向外;有一质量m=1×10-2kg、电荷量q=4×10-5C的带正电小球自O点沿与水平线成45°角以v0=4m/s的速度射入复合场中,之后小球恰好从P点进入电场强度E2=2 500N/C,方向水平向左的第二个匀强电场中.不计空气阻力,g取10m/s2.求: