Question

如图所示，半径为2R的圆弧轨道AB和半径为R的圆弧轨道BC相切于B点，两轨道置于竖直平面内，在C点的正上方有一厚度不计的旋转平台，沿平台的一条直径上开有两个小孔P、Q，两孔离轴心等距离，旋转时两孔均能到达C点正上方，平台离C点的高度为R，质量为2m的小球1自A点由静止开始下落，在B点与质量为m的2球作弹性碰撞，碰后2球过C点，且恰能无碰撞穿过小孔P.

(1)两球第一次碰撞后2球的速度大小

（2）欲使2球能从小孔Q落下，则平台的角速度w应满足什么条件？（不计所有阻力）

 

Answer 1

【答案】

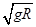（1）8/3（2）

【解析】

试题分析：（1）设小球1在B点速度大小为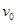则满足：

2mg*2R=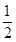2mv₀²-0

得v₀＝＝2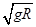 

两球碰撞过程满足动量守恒和能量守恒,设两球碰后速度大小为v₁和v₂，则：

2m v₀＝2 m v₁＋m v₂

且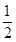2m v₀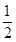²＝2 m v₁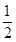²＋m v₂²

所以v₂＝4 v₀／3＝8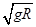/3 

 

（2）对碰后B球上升至P的过程，由能量守恒：

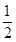m v₂²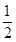＝m v_P²+2mgR

v_P＝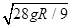 

而小球做竖直上抛的时间满足：  

又因为 

所以角速度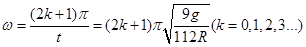

考点：动量守恒定律

点评：本题考查了在碰撞过程中的动量守恒定律的应用。应用程度较高，在运用过程中要结合能量综合考虑。