题目内容
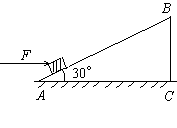
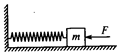
如图14所示,斜面的倾角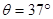 ,斜面顶端离地面高为
,斜面顶端离地面高为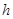 ,轻弹簧左端固定,右端恰在斜面底端处,弹簧的劲度系数为
,轻弹簧左端固定,右端恰在斜面底端处,弹簧的劲度系数为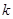 ,小滑块的质量为
,小滑块的质量为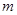 ,滑块与斜面间的动摩擦因数为
,滑块与斜面间的动摩擦因数为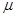 ,水平面光滑。滑块从斜面的顶端由静止释放,忽略滑块达斜面底端时速度大小的变化,弹簧始终在弹性限度内。(
,水平面光滑。滑块从斜面的顶端由静止释放,忽略滑块达斜面底端时速度大小的变化,弹簧始终在弹性限度内。(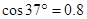 ,
,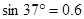 。)
。)
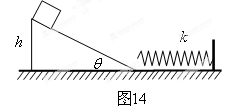
求:(1)滑块第一次达斜面底端时的速度。
(2)弹簧的最大形变量。
(3)从开始下滑到最终静止滑块沿斜面运动的总路程。
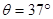 ,斜面顶端离地面高为
,斜面顶端离地面高为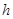 ,轻弹簧左端固定,右端恰在斜面底端处,弹簧的劲度系数为
,轻弹簧左端固定,右端恰在斜面底端处,弹簧的劲度系数为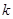 ,小滑块的质量为
,小滑块的质量为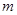 ,滑块与斜面间的动摩擦因数为
,滑块与斜面间的动摩擦因数为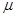 ,水平面光滑。滑块从斜面的顶端由静止释放,忽略滑块达斜面底端时速度大小的变化,弹簧始终在弹性限度内。(
,水平面光滑。滑块从斜面的顶端由静止释放,忽略滑块达斜面底端时速度大小的变化,弹簧始终在弹性限度内。(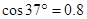 ,
,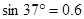 。)
。)
求:(1)滑块第一次达斜面底端时的速度。
(2)弹簧的最大形变量。
(3)从开始下滑到最终静止滑块沿斜面运动的总路程。
(1)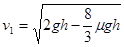 (2)
(2)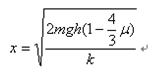 (3)
(3)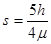
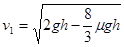 (2)
(2)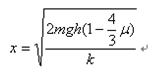 (3)
(3)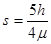
(1)设滑块达斜面底端时的速度为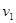 。由动能定理得:
。由动能定理得:
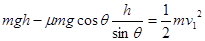
带入数值解得: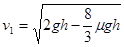

(3)滑块从开始释放到最终静止在斜面的底端过程,设滑块沿斜面运动的总路程为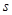
由动能定理得:
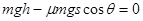
解得: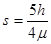
本题考查能量守恒定律和功能关系,先由下滑过程应用动能定理求得接触弹簧前的速度,再根据动能定理求得把弹簧压缩到最短的弹性势能,求得弹簧压缩量
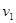 。由动能定理得:
。由动能定理得: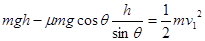
带入数值解得:
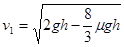

(3)滑块从开始释放到最终静止在斜面的底端过程,设滑块沿斜面运动的总路程为
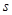
由动能定理得:
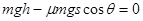
解得:
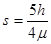
本题考查能量守恒定律和功能关系,先由下滑过程应用动能定理求得接触弹簧前的速度,再根据动能定理求得把弹簧压缩到最短的弹性势能,求得弹簧压缩量

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
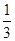 g竖直下落到地面,在此过程中
g竖直下落到地面,在此过程中 mgh
mgh
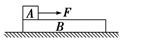
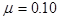 ,斜面的倾角
,斜面的倾角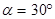 ,斜面斜边的长度为2.0m,试求:
,斜面斜边的长度为2.0m,试求: