题目内容
1.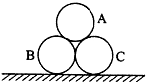 如图所示,三个完全相同质量均为m的圆柱状物体静止堆放在粗糙水平面上,B、C接触但不相互挤压,不考虑A与B、C之间的摩擦,下列说法正确的是( )
如图所示,三个完全相同质量均为m的圆柱状物体静止堆放在粗糙水平面上,B、C接触但不相互挤压,不考虑A与B、C之间的摩擦,下列说法正确的是( )| A. | A、B之间的弹力大小为$\sqrt{3}$mg | |
| B. | B与地面之间没有摩擦力 | |
| C. | 地面对c的摩擦力大小为$\frac{\sqrt{3}}{6}$mg | |
| D. | B与地面之间的动摩擦因数有可能为$\frac{\sqrt{3}}{10}$ |
分析 对A进行受力分析,A处于平衡状态,合力为零,根据平衡条件求出A、B之间的弹力大小,对B受力分析,根据B处于静止状态分析B与地面间是否有摩擦力,根据对称性可知,BC的受到的摩擦力大小相等,方向相反,对B受力分析求解摩擦力,B受到的是静摩擦力,根据静摩擦力小于等于滑动摩擦力求解动摩擦因数的范围.
解答 解:A、对A进行受力分析,如图所示:
A处于平衡状态,合力为零,则有:
${N}_{2}cos\frac{θ}{2}=\frac{1}{2}mg$
解得:${N}_{2}=\frac{\frac{1}{2}mg}{cos30°}=\frac{\sqrt{3}}{3}mg$,故A错误;
B、对B受力分析,受到重力、地面的支持力、A对B斜向下的压力,要使B受力平衡,则必须受到地面对B的水平向右的摩擦力,故B错误;
C、根据对称性可知,C受到的摩擦力与B受到的摩擦力大小相等,
对B根据平衡条件得:
f=${N}_{2}cos60°=\frac{\sqrt{3}}{3}mg×\frac{1}{2}=\frac{\sqrt{3}}{6}mg$,所以地面对C的摩擦力大小为$\frac{\sqrt{3}}{6}$mg,故C正确;
D、根据平衡条件可知,地面对B的支持力${F}_{N}=mg+{N}_{2}sin60°=mg+\frac{\sqrt{3}}{3}mg×\frac{\sqrt{3}}{2}$=$\frac{3}{2}mg$
B受到的是静摩擦力,则有μFN≥f
解得:$μ≥\frac{\frac{\sqrt{3}}{6}mg}{\frac{3}{2}mg}=\frac{\sqrt{3}}{9}$,故D错误.
故选:C
点评 本题关键是对物体受力分析,根据共点力平衡条件求解,解题时注意BC具有对称性,难度适中.

| A. | a种方式先到达 | B. | b种方式先到达 | ||
| C. | c种方式先到达 | D. | 条件不足,无法确定 |
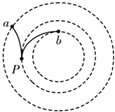 图中虚线是某电场中的一簇等势线.两个带电粒子从P点均沿等势线的切线方向射入电场,粒子运动的部分轨迹如图中实线所示.若粒子仅受电场力的作用,下列说法中正确的是( )
图中虚线是某电场中的一簇等势线.两个带电粒子从P点均沿等势线的切线方向射入电场,粒子运动的部分轨迹如图中实线所示.若粒子仅受电场力的作用,下列说法中正确的是( )| A. | a、b两点的电场强度大小关系b点大 | |
| B. | a、b两点的电势关系y=v0t | |
| C. | 粒子从P运动到a的过程中,电势能增大 | |
| D. | 粒子从P运动到b的过程中,动能增大 |
| A. | 物体运动的速度改变越大,它的加速度一定越大 | |
| B. | 加速度是矢量,速度是标量 | |
| C. | 物体运动的速度改变越小,它的加速度一定越小 | |
| D. | 物体运动的速度改变越快,它的加速度一定越大 |

| A. | 图线1表示物体做曲线运动 | |
| B. | 两图象中,t2、t4时刻分别表示2、4开始反向运动 | |
| C. | v-t图象中0至t3时间内3和4的平均速度大小相等 | |
| D. | s-t图象中t1时刻v1>v2 |
 如图为某工厂生产流水线上的水平传输装置的俯视图,它由传送带和转盘组成.物品从A处无初速、等时间间隔地放到传送带上,运动到B处后进入匀速转动的转盘,且恰好随转盘一起运动而无相对滑动,到C处取走物品.已知在转盘上物品到转轴O的距离R=4m,传送带的传输速度和转盘上距O为R处的线速度大小相等,物品与传送带间的动摩擦因数μ1=0.2,与转盘间的动摩擦因数μ2=0.4,物品在转盘上的最大静摩擦力可视为与滑动摩擦力大小相等,取g=10m/s2,求:
如图为某工厂生产流水线上的水平传输装置的俯视图,它由传送带和转盘组成.物品从A处无初速、等时间间隔地放到传送带上,运动到B处后进入匀速转动的转盘,且恰好随转盘一起运动而无相对滑动,到C处取走物品.已知在转盘上物品到转轴O的距离R=4m,传送带的传输速度和转盘上距O为R处的线速度大小相等,物品与传送带间的动摩擦因数μ1=0.2,与转盘间的动摩擦因数μ2=0.4,物品在转盘上的最大静摩擦力可视为与滑动摩擦力大小相等,取g=10m/s2,求: