题目内容
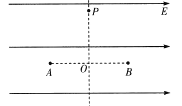
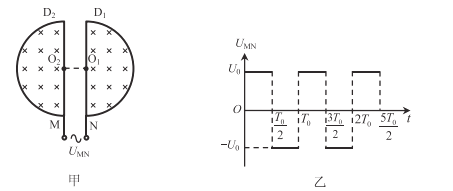
【题目】如图甲,两个半径足够大的D形金属盒D1、D2正对放置,O1、O2分别为两盒的圆心,盒内区域存在与盒面垂直的匀强磁场。加在两盒之间的电压变化规律如图乙,正反向电压的大小均为Uo,周期为To,两盒之间的电场可视为匀强电场。在t=0时刻,将一个质量为m、电荷量为q(q>0)的粒子由O2处静止释放,粒子在电场力的作用下向右运动,在![]() 时刻通过O1.粒子穿过两D形盒边界M、N时运动不受影响,不考虑由于电场变化而产生的磁场的影响,不计粒子重力。
时刻通过O1.粒子穿过两D形盒边界M、N时运动不受影响,不考虑由于电场变化而产生的磁场的影响,不计粒子重力。
(1)求两D形盒边界M、N之间的距离;
(2)若D1盒内磁场的磁感应强度![]() ,且粒子在D1、D2盒内各运动一次后能到达 O1,求D2盒内磁场的磁感应强度;
,且粒子在D1、D2盒内各运动一次后能到达 O1,求D2盒内磁场的磁感应强度;
(3)若D2、D2盒内磁场的磁感应强度相同,且粒子在D1、D2盒内各运动一次后在t= 2To时刻到达Ol,求磁场的磁感应强度。
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)设两盒之间的距离为d,盒间电场强度为E,粒子在电场中的加速度为a,则有
U0=Ed
qE=ma
![]()
联立解得
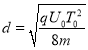
(2)设粒子到达O1的速度为v1,在D1盒内运动的半径为R1,周期为T1,时间为t1,则有
![]()
![]()
![]()
![]()
可得
t1=T0
故粒子在![]() 时刻回到电场;
时刻回到电场;
设粒子经电场再次加速后以速度v2进入D2盒,由动能定理
![]()
设粒子在D2盒内的运动半径为R2,则
![]()
粒子在D1D2盒内各运动一次后能到达O2应有
R2=R1
联立各式可得
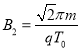
(3)依题意可知粒子在D1D2盒内运动的半径相等;又
![]()
故粒子进入D2盒内的速度也为v1;可判断出粒子第二次从O2运动到O1的时间也为![]() 粒子的运动轨迹如图;
粒子的运动轨迹如图;
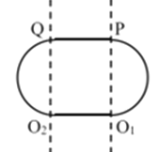
粒子从P到Q先加速后减速,且加速过程的时间和位移均相等,设加速过程的时间为t2,则有
![]()
则粒子每次在磁场中运动的时间
![]()
又
![]()
![]()
联立各式解得
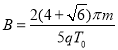

练习册系列答案
相关题目