题目内容
11.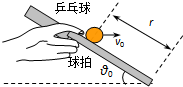 某校在水平直道举行托乒乓球跑步比赛,比赛距离为S.某同学将球置于球拍中心,从静止开始做匀加速直线运动,加速度大小为a,当速度达到v0时,再以v0做匀速直线运动跑至终点.整个过程中球一直保持在球拍中心不动.在匀速直线运动阶段保持球拍的倾角为θ0,如图所示,设球在运动中受到的空气阻力大小与其速度大小成正比,方向与运动方向相反,不计球与球拍间的摩擦,球的质量为m,重力加速度为g.
某校在水平直道举行托乒乓球跑步比赛,比赛距离为S.某同学将球置于球拍中心,从静止开始做匀加速直线运动,加速度大小为a,当速度达到v0时,再以v0做匀速直线运动跑至终点.整个过程中球一直保持在球拍中心不动.在匀速直线运动阶段保持球拍的倾角为θ0,如图所示,设球在运动中受到的空气阻力大小与其速度大小成正比,方向与运动方向相反,不计球与球拍间的摩擦,球的质量为m,重力加速度为g.(1)求空气阻力大小与球速大小的比例系数k;
(2)求在加速跑阶段球拍倾角θ随速度v变化的关系式;
(3)整个匀速跑阶段,若该同学速度仍为v0,而球拍的倾角比θ0大了β并保持不变,不计球在球拍上的移动引起的空气阻力变化,为保证到达终点前球不从球拍上距离中心为r的下边沿掉落,求β应满足的条件.
分析 (1)在匀速运动阶段,受力平衡,根据平衡条件列式即可求解;
(2)加速阶段,设球拍对球的支持力为N′,根据牛顿第二定律即可求解;
(3)根据牛顿第二定律求出球沿球拍面下滑的加速度,当球运动的位移小于等于r时,球不从球拍上掉落,根据运动学基本公式列式即可求解.
解答 解:(1)在匀速运动阶段,有 mgtanθ0=kv0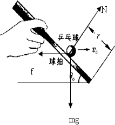
得k=$\frac{mgtan{θ}_{0}}{{v}_{0}}$
(2)加速阶段,设球拍对球的支持力为N′,有
N′sinθ-kv=ma
N′cosθ=mg
得tanθ=$\frac{a}{g}$+$\frac{v}{{v}_{0}}$tanθ0
(3)以速度v0匀速运动时,设空气阻力与重力的合力为F,有F=$\frac{mg}{cos{θ}_{0}}$
球拍倾角为θ0+β时,空气阻力与重力的合力不变.
设球沿球拍面下滑的加速度大小为a′,有Fsinβ=ma′
设匀速跑阶段所用时间为t,有
t=$\frac{s}{{v}_{0}}$-$\frac{{v}_{0}}{2a}$
球不从球拍上掉落的条件 $\frac{1}{2}$a′t2≤r
得 $sinβ≤\frac{{2rcos{θ_0}}}{{g{{(\frac{s}{v_0}-\frac{v_0}{2a})}^2}}}$.
答:
(1)空气阻力大小与球速大小的比例系数k为$\frac{mgtan{θ}_{0}}{{v}_{0}}$;
(2)在加速跑阶段球拍倾角θ随速度v变化的关系式为tanθ=$\frac{a}{g}$+$\frac{v}{{v}_{0}}$tanθ0;
(3)β应满足的条件为 $sinβ≤\frac{{2rcos{θ_0}}}{{g{{(\frac{s}{v_0}-\frac{v_0}{2a})}^2}}}$.
点评 本题主要考查了牛顿第二定律及运动学基本公式的应用,关键要求同学们能正确受力分析.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案| A. | $\frac{{{U}_{1}}^{2}}{R}$ | B. | $\frac{({U}_{1}-{U}_{2})^{2}}{R}$ | C. | I2R | D. | U1I |
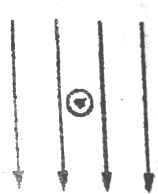
| A. | 向上 | B. | 向下 | C. | 向左 | D. | 向右 |
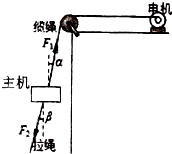 如图所示,高层住宅外安装空调主机时,电机通过缆绳牵引主机沿竖直方向匀速上升.为避免主机与阳台、窗户碰撞,通常会用一根拉绳拽着主机,地面上拽拉绳的人通过移动位置,使拉绳与竖直方向的夹角β保持不变.则在提升主机过程中(题中缆绳和拉绳均视为轻质绳),下列结论正确的是( )
如图所示,高层住宅外安装空调主机时,电机通过缆绳牵引主机沿竖直方向匀速上升.为避免主机与阳台、窗户碰撞,通常会用一根拉绳拽着主机,地面上拽拉绳的人通过移动位置,使拉绳与竖直方向的夹角β保持不变.则在提升主机过程中(题中缆绳和拉绳均视为轻质绳),下列结论正确的是( )| A. | 缆绳拉力F1和拉绳拉力F2都增大 | |
| B. | 缆绳拉力F1和拉绳拉力F2都不变 | |
| C. | 缆绳与竖直方向的夹角α可能大于角β | |
| D. | 缆绳拉力F1的功率保持不变 |
| A. | 1m/s | B. | 2 m/s | C. | 3 m/s | D. | 4 m/s |
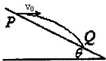 如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上的P点,沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为θ,已知该星球半径为R,不考虑其他可能存在的阻力,万有引力常量为G.求该星球的密度和该星球上的第一宇宙速度.
如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上的P点,沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为θ,已知该星球半径为R,不考虑其他可能存在的阻力,万有引力常量为G.求该星球的密度和该星球上的第一宇宙速度.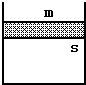 如图所示,在大气中的一个汽缸中封闭有一定的气体,汽缸的活塞的质量m=2kg,面积s=20cm2.若大气压强取p0=1×105Pa,则汽缸中气体的压强是多大?(g取10m/s2)
如图所示,在大气中的一个汽缸中封闭有一定的气体,汽缸的活塞的质量m=2kg,面积s=20cm2.若大气压强取p0=1×105Pa,则汽缸中气体的压强是多大?(g取10m/s2)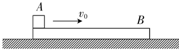 物体A的质量m1=1kg,静止在光滑的水平面上的木板B的质量m2=0.5kg、长L=1m,A与B之间的动摩擦因数μ=0.2.某时刻A以v0=4m/s的初速度滑上木板B的上表面,从木板的另一端滑下.(重力加速度g取10m/s2)
物体A的质量m1=1kg,静止在光滑的水平面上的木板B的质量m2=0.5kg、长L=1m,A与B之间的动摩擦因数μ=0.2.某时刻A以v0=4m/s的初速度滑上木板B的上表面,从木板的另一端滑下.(重力加速度g取10m/s2)