Question

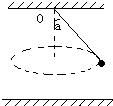
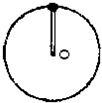
如图，长为R的轻杆一端固定着质量为m的小球，以另一端为轴在竖直面内匀速转动，求下列两种情况小球转动的角速度ω的值．
（1）当球转至最高点时，若小球对棒作用力为0；
（2）当球转至最高点时，若小球对棒作用力为

mg

2

．

Answer 1

（1）若小球对棒作用力为0则只有重力提供向心力，根据牛顿第二定律：mg=mω²R
得：ω=

g R

（2）若小球对棒作用力为拉力

mg

2

，即棒对小球的作用力也为拉力，根据牛顿第二定律：
F+mg=mω²R
得：ω=

3g 2R

若小球对棒作用力为支持力

mg

2

，即棒对小球的作用力为支持力，根据牛顿第二定律：
mg-F=mω²R
得：ω=

g 2R

答：（1）当球转至最高点时，若小球对棒作用力为0角速度为

g R

；
（2）当球转至最高点时，若小球对棒作用力为

mg

2

角速度为

3g 2R

或

g 2R

．