Question

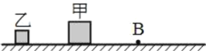
【题目】如图，水平面上从B点往左都是光滑的，从B点往右都是粗糙的．质量分别为M和m的两个小物块甲和乙（可视为质点），与粗糙水平面间的动摩擦因数分别为μ甲和μ乙，在光滑水平面上相距L以相同的速度同时开始向右运动，它们在进入粗糙区域后最后静止。设静止后两物块间的距离为s，甲运动的总时间为t1、乙运动的总时间为t2，则以下说法中正确的是

A.若M=m，μ甲=μ乙，则s=L

B.若μ甲=μ乙，无论M、m取何值，总是s=0

C.若μ甲＜μ乙，M＞m，则可能t1=t2

D.若μ甲＜μ乙，无论M、m取何值，总是t1＜t2

Answer 1

【答案】BC

【解析】

A．由动能定理可知：

若，，则两物体在粗糙地面上滑动的位移相同，故二者的距离为零，故A错误；

B．由动能定理可知：

解得：

滑行距离与质量无关，故若，无论、取何值，总是，故B正确；

CD．两物体在粗糙斜面上的加速度：

则从点运动到停止的时间：

若，则有：

因乙离点较远，故可能有：

故C正确，D错误；

故选BC。