题目内容
如图,长2米的轻绳,一端系在悬点O上,一端系一质量m1为0.1kg的小球。小球从A点由静止释放,已知,OA与竖直方向成53°角。小球运动到悬点O的正下方B点时,与质量m2为0.05kg的另一小球正碰,碰撞过程无能量损失。碰后瞬间,质量为m2的小球过B点下方的起电器时,带上正电,电荷量为q。水平轨道BC和光滑半圆轨道CD相切,BC长0.5米,与小球之间的动摩擦因数µ为0.1,竖直半圆轨道CD的半径R是0.2米。水平轨道BC和竖直半圆轨道CD都是绝缘材料制成,且处于场强为E=104v/m的竖直匀强电场中。如果碰后质量为m1小球对轨道无影响,而质量为m2的小球刚好能过半圆的最高点D。(g=10 m/s²,sin53°=0.8 , cos53°=0.6)
求:质量为m2的小球所带电量q是多少?

解:(16分)
A下摆: m1gL(1-cos53°)=0.5m1v2 ,∴v=4m/s
AB碰撞: m1v=m1v1+m2v2 ,
0.5m1v2 =0.5 m1v12+0.5m2v22 ,
∴v2=16/3 m/s (7分)
B减速: -μ(m2g+qE)s=0.5 m2v32-0.5m2v22 ,
B上升: 0.5 m2v32=2m2gR+2qER+0.5 m2v42 ,
B 点: m2g+qE= m2v42/ R ,
∴q=![]() ×10-4 C =7.9×10-5 C (9分)
×10-4 C =7.9×10-5 C (9分)

练习册系列答案
相关题目
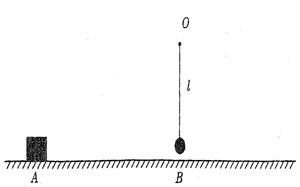
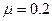 ,与A点相距s=2.25m的B点上方有一质量m=1.2kg的小球,小球被一长为
,与A点相距s=2.25m的B点上方有一质量m=1.2kg的小球,小球被一长为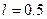 米的轻绳紧挂在O点而处于静止状态。现给滑块一瞬时冲量I=10N·s,让滑块沿水平面向右运动,此后与小球发生碰撞,碰后小球恰能在竖直平面内完成完整的圆周运动(g取10m/s2)。求:滑块最终静止在距离A点多远处?因滑块与小球碰撞而损失的机械能是多少?
米的轻绳紧挂在O点而处于静止状态。现给滑块一瞬时冲量I=10N·s,让滑块沿水平面向右运动,此后与小球发生碰撞,碰后小球恰能在竖直平面内完成完整的圆周运动(g取10m/s2)。求:滑块最终静止在距离A点多远处?因滑块与小球碰撞而损失的机械能是多少?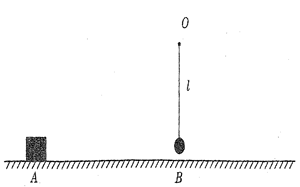
 ,与A点相距s=2.25m的B点上方有一质量m=1.2kg的小球,小球被一长为
,与A点相距s=2.25m的B点上方有一质量m=1.2kg的小球,小球被一长为 米的轻绳紧挂在O点而处于静止状态。现给滑块一瞬时冲量I=10N·s,让滑块沿水平面向右运动,此后与小球发生碰撞,碰后小球恰能在竖直平面内完成完整的圆周运动(g取10m/s2)。求:滑块最终静止在距离A点多远处?因滑块与小球碰撞而损失的机械能是多少?
米的轻绳紧挂在O点而处于静止状态。现给滑块一瞬时冲量I=10N·s,让滑块沿水平面向右运动,此后与小球发生碰撞,碰后小球恰能在竖直平面内完成完整的圆周运动(g取10m/s2)。求:滑块最终静止在距离A点多远处?因滑块与小球碰撞而损失的机械能是多少?