题目内容
17.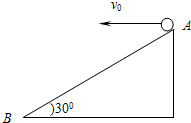 如图所示,AB为足够长的斜面,倾角为30°,小球从A点以初速度v0水平抛出,求经过多长时间小球离斜面的距离最远,最远距离是多少?
如图所示,AB为足够长的斜面,倾角为30°,小球从A点以初速度v0水平抛出,求经过多长时间小球离斜面的距离最远,最远距离是多少?
分析 将小球的运动沿着平行斜面和垂直斜面方向正交分解,垂直斜面方向做匀减速直线运动,当垂直斜面方向分速度为零时小球离斜面的距离达到最大;根据分运动公式列式求解.
解答 解:将小球的运动分解为沿斜面和垂直于斜面两个方向分运动,建立如图所示的坐标系,小球在y轴方向做匀减速运动,初速度为 vy0=v0sinθ,加速度为:ay=-gcosθ,
当垂直斜面方向的速度为零时,距离斜面最远,有:t=$\frac{{-v}_{y0}}{{a}_{y}}=\frac{{v}_{0}sinθ}{gcosθ}=\frac{{v}_{0}tanθ}{g}$=$\frac{\sqrt{3}{v}_{0}}{3g}$.
小球离斜面的最大距离${y}_{m}=\frac{{{v}_{y0}}^{2}}{-2{a}_{y}}=\frac{{{v}_{0}}^{2}si{n}^{2}θ}{2gcosθ}$=$\frac{{{v}_{0}}^{2}}{4\sqrt{3}g}$.
答:经过$\frac{\sqrt{3}{v}_{0}}{3g}$时间小球距离斜面最远,最远距离为$\frac{{{v}_{0}}^{2}}{4\sqrt{3}g}$.
点评 本题关键是采用正交分解法研究平抛运动,正交分解的方向可以灵活选择,同时要抓住两个方向分位移的关系,运用运动学公式处理.

练习册系列答案
相关题目
5. 如图所示,质量为m的小球穿在足够长的水平固定直杆上处于静止状态,现对小球同时施加水平向右的恒力F0和竖直向上的力F,使小球从静止开始向右运动,其中竖直向上的力F大小始终与小球的速度成正比,即F=kυ(图中未标出).已知小球与杆间的动摩擦因数为μ,下列说法中正确的是( )
如图所示,质量为m的小球穿在足够长的水平固定直杆上处于静止状态,现对小球同时施加水平向右的恒力F0和竖直向上的力F,使小球从静止开始向右运动,其中竖直向上的力F大小始终与小球的速度成正比,即F=kυ(图中未标出).已知小球与杆间的动摩擦因数为μ,下列说法中正确的是( )
 如图所示,质量为m的小球穿在足够长的水平固定直杆上处于静止状态,现对小球同时施加水平向右的恒力F0和竖直向上的力F,使小球从静止开始向右运动,其中竖直向上的力F大小始终与小球的速度成正比,即F=kυ(图中未标出).已知小球与杆间的动摩擦因数为μ,下列说法中正确的是( )
如图所示,质量为m的小球穿在足够长的水平固定直杆上处于静止状态,现对小球同时施加水平向右的恒力F0和竖直向上的力F,使小球从静止开始向右运动,其中竖直向上的力F大小始终与小球的速度成正比,即F=kυ(图中未标出).已知小球与杆间的动摩擦因数为μ,下列说法中正确的是( )| A. | 小球先做加速度增大的加速运动,后做加速度减小的加速运动,直到最后做匀速运动 | |
| B. | 小球先做加速度减小的加速运动,后做加速度增大的减速运动直到静止 | |
| C. | 小球的最大加速度为$\frac{F_0}{m}$ | |
| D. | 小球的最大速度为$\frac{{{F_0}+μmg}}{μk}$,恒力F0的最大功率为$\frac{{F_0^2+{F_0}μmg}}{2μk}$ |
2. 如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接一正弦交变电源,电压u=311sin(100πt)V.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )
如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接一正弦交变电源,电压u=311sin(100πt)V.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )
 如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接一正弦交变电源,电压u=311sin(100πt)V.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )
如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接一正弦交变电源,电压u=311sin(100πt)V.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )| A. | 当R2所在处出现火警时,电阻R1的功率变小 | |
| B. | 当R2所在处出现火警时,电压表V2的示数变大 | |
| C. | 当R2所在处出现火警时,电流表A的示数变大 | |
| D. | 电压表V1示数为31.1 V |
6.随着“嫦娥工程”的实施,我国宇航员登上月球已不是梦想.假如宇航员登上月球并在月球表面附近以初速度v0竖直向上抛出一个小球,经时间t后回到出发点.已知月球的半径为R,万有引力常量为G,下列说法正确的是( )
| A. | 月球的质量为$\frac{{2{v_0}{R^2}}}{Gt}$ | |
| B. | 月球表面的重力加速度为$\frac{v_0}{t}$ | |
| C. | 宇航员在月球表面获得$\sqrt{\frac{{{v_0}R}}{t}}$的速度就可能离开月球表面围绕月球做圆周运动 | |
| D. | 宇航员在月球表面附近绕月球做匀速圆周运动的绕行周期为$π\sqrt{\frac{Rt}{v_0}}$ |
7.列属于离心现象的是( )
| A. | 链球运动员加速旋转到一定速度后将链球抛开 | |
| B. | 汽车紧急刹车时,乘客身体向前倾 | |
| C. | 水平抛出的物体,做平抛运动 | |
| D. | 锤头松了,将锤柄在石头上磕几下就可以把柄安牢 |
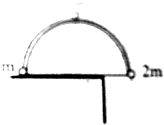 如图所示,质量分别为m和2m的两个小物体可视为质点,用轻质细绳连接,跨过光滑半圆柱体,轻的与桌面接触,重的恰好与圆心一样高,若无初速地释放,则物体m上升到圆弧最高点时小球的速度是多少?(物体大小忽略不计)
如图所示,质量分别为m和2m的两个小物体可视为质点,用轻质细绳连接,跨过光滑半圆柱体,轻的与桌面接触,重的恰好与圆心一样高,若无初速地释放,则物体m上升到圆弧最高点时小球的速度是多少?(物体大小忽略不计) 有一个单摆,当做小角度(θ<5°)摆动时,摆球的振动图象如图所示,求摆球摆到最低点时的速度为0.45m/s.
有一个单摆,当做小角度(θ<5°)摆动时,摆球的振动图象如图所示,求摆球摆到最低点时的速度为0.45m/s. 如图所示,一根张紧的水平弹性长绳上的a、b两点,相距4.5m,a点在b点的左方.当一列简谐波沿此长绳向右传播时,若a点的位移达到正向最大时,b点的位移恰好为零,且向下运动;此后再经过t=3.0s,a点恰好第二次通过平衡位置,设该波的波长2m≤λ≤3m.求
如图所示,一根张紧的水平弹性长绳上的a、b两点,相距4.5m,a点在b点的左方.当一列简谐波沿此长绳向右传播时,若a点的位移达到正向最大时,b点的位移恰好为零,且向下运动;此后再经过t=3.0s,a点恰好第二次通过平衡位置,设该波的波长2m≤λ≤3m.求