题目内容
17. 如图所示,在沿水平方向的匀强电场中有一固定点O,用一根L=0.4m的绝缘细线把质量为m=0.10kg,带有q=3.0×10-4C正电荷的金属小球悬挂在O点,小球静止在B点时细线与竖直方向的夹角为θ=37°,现将小球拉至位置A使细线水平后由静止释放,求:
如图所示,在沿水平方向的匀强电场中有一固定点O,用一根L=0.4m的绝缘细线把质量为m=0.10kg,带有q=3.0×10-4C正电荷的金属小球悬挂在O点,小球静止在B点时细线与竖直方向的夹角为θ=37°,现将小球拉至位置A使细线水平后由静止释放,求:(1)该电场的场强是多大?
(2)小球通过最低点C时的速度大小;
(3)小球通过最低点C时细线对小球的拉力大小;
(4)小球从A到C点的过程中的最大速度(g=10m/s2)
分析 (1)根据共点力平衡求出电场强度的大小.
(2)根据动能定理求出运动到C点的速度.
(3)根据牛顿第二定律,抓住径向的合力提供向心力求出拉力的大小.
(4)B点为等效最低点,速度最大,根据动能定理求出最大速度.
解答 解:(1)小球在B点处于静止状态,对小球进行受力分析,根据平衡条件得:
F=qE=mgtanθ
解得E=$\frac{mgtanθ}{q}$=$\frac{1×\frac{3}{4}}{3×1{0}^{-4}}N/C=2.5×1{0}^{3}N/C$.
(2)根据动能定理得,mgL-qEL=$\frac{1}{2}m{{v}_{C}}^{2}$,
代入数据解得vC=$\sqrt{2}$m/s.
(3)根据牛顿第二定律得,$T-mg=m\frac{{{v}_{C}}^{2}}{L}$,
解得T=$mg+m\frac{{{v}_{C}}^{2}}{L}=1+0.1×\frac{2}{0.4}N=1.5N$.
(4)当小球运动到B点时,速度最大,根据动能定理得,
$mgLcos37°-qEL(1-sin37°)=\frac{1}{2}m{{v}_{m}}^{2}$,
代入数据解得vm=2m/s.
答:(1)该电场的场强是2.5×103N/C;
(2)小球通过最低点C时的速度大小为$\sqrt{2}m/s$;
(3)小球通过最低点C时细线对小球的拉力大小为1.5N;
(4)小球从A到C点的过程中的最大速度为2m/s.
点评 本题主要考查了平衡条件、动能定理及向心力公式的直接应用,第三问略微难一点,要考虑等效最低点问题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
6.如图为做简谐运动质点的振动图象.下列说法正确的是( )


| A. | 图中曲线表示质点运动的轨迹 | |
| B. | 0.7s时,质点的振动方向沿x轴负方向 | |
| C. | 该简谐运动的表达式为x=0.08cos5πt(m) | |
| D. | 从0.25s到0.35s,质点运动的速度方向不变,加速度方向也不变 |
12.教师在黑板上画圈,圆规脚之间的距离是25cm,他保持这个距离不变,让粉笔在黑板上匀速的画了一个圈.粉笔的线速度是2.5m/s,关于粉笔的运动,有下列说法正确的是( )
| A. | 角速度是0.1rad/s | B. | 转速大于2r/s | ||
| C. | 周期是0.628s | D. | 向心加速度是2.5m/s2 |
9. 2011年11月01日5时58分07秒,我国成功发射神州八号飞船,它将与天宫一号实现空中对接,从而建立我国第一个空间实验室.假如神舟八号与天宫一号对接前所处的轨道如图所示,当它们处于如图所示的轨道运行时,下列说法正确的是( )
2011年11月01日5时58分07秒,我国成功发射神州八号飞船,它将与天宫一号实现空中对接,从而建立我国第一个空间实验室.假如神舟八号与天宫一号对接前所处的轨道如图所示,当它们处于如图所示的轨道运行时,下列说法正确的是( )
 2011年11月01日5时58分07秒,我国成功发射神州八号飞船,它将与天宫一号实现空中对接,从而建立我国第一个空间实验室.假如神舟八号与天宫一号对接前所处的轨道如图所示,当它们处于如图所示的轨道运行时,下列说法正确的是( )
2011年11月01日5时58分07秒,我国成功发射神州八号飞船,它将与天宫一号实现空中对接,从而建立我国第一个空间实验室.假如神舟八号与天宫一号对接前所处的轨道如图所示,当它们处于如图所示的轨道运行时,下列说法正确的是( )| A. | 神舟八号的运行加速度比天宫一号的小 | |
| B. | 神舟八号的运行速度比天宫一号的小 | |
| C. | 神舟八号的运行周期比天宫一号的短 | |
| D. | 神舟八号从图示轨道运动到与“天宫一号”对接过程中,机械能守恒 |
6.下列关于电磁场和电磁波的认识中,正确的是( )
| A. | 电场和磁场总是相互联系着的,统称为电磁场 | |
| B. | 电磁波和机械波一样,离开由分子、原子组成的介质就不能传播 | |
| C. | 均匀变化的电场在它周围空间将产生均匀变化的磁场 | |
| D. | 只要空间某区域有振荡的电场或磁场,就能产生电磁波 |
7.下列关于速度与加速度的说法中,正确的是( )
| A. | 物体的速度越大,其加速度也越大 | |
| B. | 物体的加速度大,其速度一定大 | |
| C. | 物体的速度变化量越大,其加速度就越大 | |
| D. | 物体的速度变化越快,其加速度就越大 |
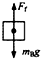
 如图所示,质量mA>mB的两物体A,B叠放在一起,靠着竖直墙面,已知两物体与墙面的动摩擦因数μA>μB,让他们由静止释放.在沿粗糙墙面下落过程中,物体B的受力示意图是( )
如图所示,质量mA>mB的两物体A,B叠放在一起,靠着竖直墙面,已知两物体与墙面的动摩擦因数μA>μB,让他们由静止释放.在沿粗糙墙面下落过程中,物体B的受力示意图是( )
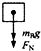

 在“油膜法估测油酸分子的大小”实验中,有下列实验步骤:
在“油膜法估测油酸分子的大小”实验中,有下列实验步骤: 光滑水平面上,一个水平长木板与半径R未知的半圆组成如图所示的装置,装置质量M=5kg.在装置的右端放一质量为m=1kg的小滑块(可视为质点),小滑块与长木板间的动摩擦因数μ=0.5,装置与小滑块一起以v0=10m/s的速度向左运动.现给装置加一个F=55N向右的水平推力,小滑块与木板发生相对滑动,当小滑块滑至长木板左端A时,装置速度恰好减速为0,此时撤去外力F并将装置锁定不动.小滑块继续沿半圆形轨道运动,且恰好能通过轨道最高点B.滑块脱离半圆形轨道后又落回长木板.已知小滑块在通过半圆形轨道时克服摩擦力做功Wf=2.5J.g取10m/s2.求:
光滑水平面上,一个水平长木板与半径R未知的半圆组成如图所示的装置,装置质量M=5kg.在装置的右端放一质量为m=1kg的小滑块(可视为质点),小滑块与长木板间的动摩擦因数μ=0.5,装置与小滑块一起以v0=10m/s的速度向左运动.现给装置加一个F=55N向右的水平推力,小滑块与木板发生相对滑动,当小滑块滑至长木板左端A时,装置速度恰好减速为0,此时撤去外力F并将装置锁定不动.小滑块继续沿半圆形轨道运动,且恰好能通过轨道最高点B.滑块脱离半圆形轨道后又落回长木板.已知小滑块在通过半圆形轨道时克服摩擦力做功Wf=2.5J.g取10m/s2.求: