题目内容
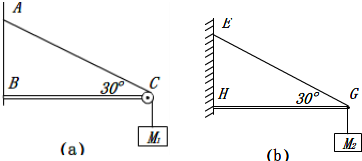
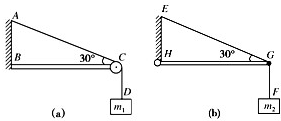
如图（a）所示，轻绳AD跨过固定在水平横梁BC右端的定滑轮，挂住一个质量为M1的物体．已知∠ACB=30°．图（b）中轻杆HG一端用铰链固定在竖直墙上，另一端G通过细绳EG拉住，EG与水平方向也成30°角，轻杆的G点用细绳GF拉住一个质量为M2的物体．求细绳AC段的张力F1与细绳EG段的张力F2之比．
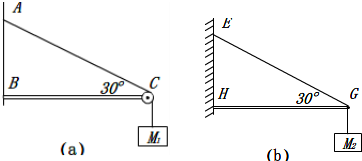
解：在图（a）中，因定滑轮不省力，则得：F1=M1g．
在图（b）中，以G点为研究对象，根据平衡条件得：
F2sin30°=M2g
则得：F2=2M2g
故得：
=
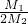
答：细绳AC段的张力F1与细绳EG段的张力F2之比为M1：2M2．
分析：根据定滑轮的力学特性，可知a图中，细绳AC段的张力等于物体的重力．
b图中，以C点为研究对象，根据平衡条件求解细绳EG段的张力F2．再求张力之比．
点评：本题首先要抓住定滑轮不省力的特点，其次要根据平衡条件，以G点为研究对象，按力平衡问题的一般步骤求解细绳EG的张力．
在图（b）中，以G点为研究对象，根据平衡条件得：
F2sin30°=M2g
则得：F2=2M2g
故得：
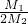
=答：细绳AC段的张力F1与细绳EG段的张力F2之比为M1：2M2．
分析：根据定滑轮的力学特性，可知a图中，细绳AC段的张力等于物体的重力．
b图中，以C点为研究对象，根据平衡条件求解细绳EG段的张力F2．再求张力之比．
点评：本题首先要抓住定滑轮不省力的特点，其次要根据平衡条件，以G点为研究对象，按力平衡问题的一般步骤求解细绳EG的张力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
BO垂直，BO与竖直方向的夹角为θ，OC连接重
物，则( )
