��Ŀ����
����Ŀ����ͼ��ʾ,�����뾶ΪR���ķ�֮һԲ�����ɵĹ⻬ϸ�ܵ�ABC��ֱ����,�ҹ̶��ڹ⻬ˮƽ����,Բ������O1O2ˮƽ���ᵯ����˹̶�����ֱ������,�Ҷ�������Ϊm��С��Ӵ�����˩��,С���ֱ����С�ڹܵ��ھ���,��ΪR�ı���DE����ˮƽ����,������D���ܵ��Ҷ�C��ˮƽ����ΪR����ʼʱ���ɴ�������״̬,���еĵ�������Ϊ3mgR,����gΪ�������ٶȡ��������,С���뿪���ɺ����ܵ�,����C���׳���
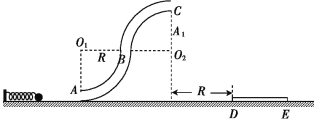
��1����С��C��ʱ�Ķ��ܺ�С��C��ʱ���ܵĵ�����
��2�����۵�������ʱ������������ʲô����,��C���׳���С����ܻ��б���DE��
���𰸡���1��mgR��mg���������£���2��![]()
��������
�����������1���������������С���˶���C����̣����ɺ�С��ϵͳ��е���غ㣬
�ɻ�е���غ㶨�ɵã�3mgR=2mgR+Ek����ã�Ek=mgR��
С���Cʱ�Ķ��ܣ�Ek��![]() mv2��
mv2��
��С��C��ʱ�����С���������ΪF��
��ţ�ٵڶ����ɵã�![]() ��
��
��ã�F=mg���������£�
��2��С���뿪C�����ƽ���˶���
��ֱ����2R��![]() gt2��
gt2��
ˮƽ����x1=v1t��
��ҪС����б��壬Ӧ���㣺R��x1��2R��
���ɵĵ������ܣ�EP=2mgR+![]() mv12��
mv12��
��������EP���㣺![]() ʱ��С����ܻ��б��壻
ʱ��С����ܻ��б��壻