题目内容
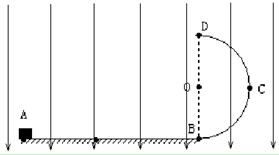
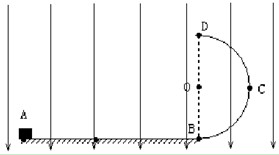
圆弧轨道AB固定于地面上，半径R＝2 m，所对圆心角为60°，其末端与逆时针转动的水平传送带相切于B点，如图所示，传送带长l＝1.5 m，速度v＝4 m/s.一质量为m＝0.1 kg的滑块从最高点A由静止开始滑下并滑上水平传送带，运动到B点时速度vB＝3 m/s.（g取10 m/s2），求：
(1)滑块在圆弧AB上克服摩擦力做的功；
(2)若滑块不从右端滑离传送带，滑块与传送带的动摩擦因数μ应满足什么条件？
(3)若传送带与滑块的动摩擦因数μ＝0.6，求滑块从B点滑到离B点最远过程中产生的热量Q.
解析 (1)A→B的过程，由动能定理得：mgR(1－cos 60°)－Wf＝
mv
①
代入数据解得Wf＝0.55 J②
(2)滑块在传送带上受到向左的摩擦力，当滑块恰好不从右端离开传送带时，
由动能定理得：－μmgl＝0－mv③
解得μ＝
＝0.3④
即μ至少为0. 3时滑块不从右端滑离传送带⑤
(3)a＝
＝6 m/s2⑥
滑块向右运动的最大距离：s1＝
＝0.75 m⑦
滑块运动时间：t＝
＝0.5 s⑧
传送带向左运动的距离：s2＝vt＝2 m⑨
则摩擦生热：Q＝Ffl相对＝μmg(s1＋s2)＝1.65 J⑩
答案 (1)0.55 J (2)μ≥0.3 (3)1.65 J
练习册系列答案
相关题目
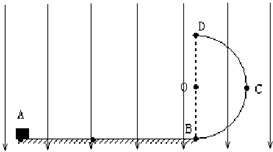如图所示，可视为质点的物体质量为m=0.4kg、电量为q=+2.0×10-2C，与水平绝缘轨道间的动摩擦因数为?=0.2，水平轨道与半径为R=0.4m的竖直光滑半圆形绝缘轨道相切于B点，AB间距为L=1.0m，轨道整体固定在地面上，空间内存在竖直向下的匀强电场，场强为E=1.0×102N/C．重力加速度g取10m/s2．物体在半圆形轨道上的B点时对轨道的压力与物体在AB间时对轨道的压力之比，称为物体运动的压力比，则：
