Question

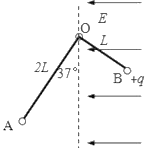
【题目】如图所示金属小球A和B固定在弯成直角的绝缘轻杆两端，A球质量为2m，不带电，B球质量为m，带正电，电量为q，OA=2L，OB=L，轻杆可绕过O点且与纸面垂直的水平轴无摩擦转动，在过O点的竖直虚线右侧区域存在着水平向左的匀强电场，此时轻杆处于静止状态，且OA与竖直方向夹角为37°，重力加速度为g。

（1）求匀强电场的电场强度大小E；

（2）若不改变场强大小，将方向变为竖直向上，则由图示位置无初速释放轻杆后，求A球刚进入电场时的速度大小v。

Answer 1

【答案】（1）；（2）。

【解析】

（1）轻杆处于静止状态时，根据力矩平衡M逆=M顺，有

mAg2Lsin37°=qELcos53°+mBgLsin53°

其中mA=2m，mB=m，匀强电场的电场强度大小

E=

（2）A、B球角速度相等，根据v=r，A球线速度是B球线速度的2倍，A球线速度为v，B球线速度为，无初速释放轻杆后，直至A球刚进入电场过程中，系统根据动能定理，有

mA g2L（1﹣cos37°）+（qE﹣mB g）Lsin37°=+

其中vA=v，vB=，解得A球刚进入电场时的速度大小

v=

答：（1）匀强电场的电场强度大小E为；（2）若不改变场强大小，将方向变为竖直向上，则由图示位置无初速释放轻杆后，A球刚进入电场时的速度大小v为。