题目内容
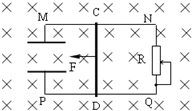
两相互平行且足够长的水平金属导轨MN、PQ放在竖直平面内，相距0.4m，左端接有平行板电容器，板间距离为0.2m，右端接滑动变阻器R。水平匀强磁场磁感应强度为10T，垂直于导轨所在平面，整个装置均处于上述匀强磁场中，导体棒CD与金属导轨垂直且接触良好，棒的电阻为1Ω，其他电阻及摩擦不计。现在用与金属导轨平行，大小为2N的恒力F使棒从静止开始运动。已知R的最大阻值为2Ω，g=10m/s2。则：⑴ 滑动变阻器阻值取不同值时，导体棒处于稳定状态时拉力的功率不一样，求导体棒处于稳定状态时拉力的最大功率。
⑵当滑动触头在滑动变阻器中点且导体棒处于稳定状态时，一个带电小球从平行板电容器左侧，以某一速度沿两板的正中间且平行于两极板射入后，在两极板间恰好做匀速直线运动；当滑动触头位于最下端且导体棒处于稳定状态时，该带电小球以同样的方式和速度射入，小球在两极板间恰好做匀速圆周运动，则小球的速度为多大。
（20分）解：（1）当棒达到匀速运动时，棒受到的安培力F1与外力F相平衡，即F=F1=BIL ① （1分）此时棒产生的电动势E=BLv，则电路中的电流。I＝ ＝ ② （1分） 由①②式得此时棒的速度 V＝ ③ （1分）拉力功率 P＝FV＝④ （1分）由④式知回路的总电阻越大时，拉力功率越大，当R=2Ω时，拉力功率最大，Pm=0.75(W) （1分）(2)当触头滑到中点即R=1Ω时，由③式知棒匀速运动的速度v1＝＝0.25(m/s) （1分）导体棒产生的感应电动势 E1=BLv1=10×0.4×0.25=1(V) （1分）电容器两极板间电压 U1＝＝0.5(V) （1分） 由于棒在平行板间做匀速直线运动，则小球必带正电,此时小球受力情况如图所示，
设小球的入射速度为v0,由平衡条件知： F+f=G即 q ＋qv0B=mg ⑤ （2分）当滑头滑至下端即R=2Ω时，棒的速度V2＝＝ (m/s) （1分）导体棒产生的感应电动势 E2=BLV2=1.5伏 （1分） 电容器两极板间的电压 U2＝＝1伏 （1分）由于小球在平行板间做匀速圆周运动,电场力与重力平衡，于是：q ＝mg ⑥ （2分）联立⑤⑥并代入数值解得 v0＝＝0.25(m/s) （1分）小球作圆周运动时洛仑兹力提供向心力,有qv0B＝m ⑦ （2分）联立⑥⑦解得小球作圆周运动的半径为r＝0.0125 m （2分）
设小球的入射速度为v0,由平衡条件知： F+f=G即 q ＋qv0B=mg ⑤ （2分）当滑头滑至下端即R=2Ω时，棒的速度V2＝＝ (m/s) （1分）导体棒产生的感应电动势 E2=BLV2=1.5伏 （1分） 电容器两极板间的电压 U2＝＝1伏 （1分）由于小球在平行板间做匀速圆周运动,电场力与重力平衡，于是：q ＝mg ⑥ （2分）联立⑤⑥并代入数值解得 v0＝＝0.25(m/s) （1分）小球作圆周运动时洛仑兹力提供向心力,有qv0B＝m ⑦ （2分）联立⑥⑦解得小球作圆周运动的半径为r＝0.0125 m （2分） 
练习册系列答案
相关题目
如图所示，光滑金属直轨道MN和PQ固定在同一水平面内，MN、PQ平行且足够长，两轨道间的宽度L=0.50m．轨道左端接一阻值R=0.50Ω的电阻．轨道处于磁感应强度大小B=0.40T，方向竖直向下的匀强磁场中．质量m=0.50kg的导体棒ab垂直于轨道放置．在沿着轨道方向向右的力F作用下，导体棒由静止开始运动，导体棒与轨道始终接触良好并且相互垂直．不计轨道和导体棒的电阻，不计空气阻力．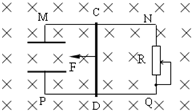
两相互平行且足够长的水平金属导轨MN、PQ放在竖直平面内，相距0.4m，左端接有平行板电容器，板间距离为0.2m，右端接滑动变阻器R．水平匀强磁场磁感应强度为10T，垂直于导轨所在平面，整个装置均处于上述匀强磁场中，导体棒CD与金属导轨垂直且接触良好，棒的电阻为1Ω，其他电阻及摩擦不计．现在用与金属导轨平行，大小为2N的恒力F使棒从静止开始运动．已知R的最大阻值为2Ω，g=10m/s2．则：
