Question

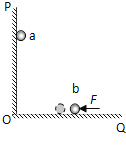
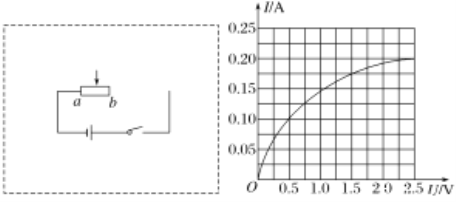
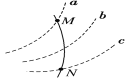
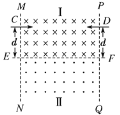
【题目】正、负电子对撞机是使正、负电子以相同速率对撞（撞前速度在同一直线上的碰撞）并进行高能物理研究的实验装置，该装置一般由高能加速器、环形储存室和对撞测量区三个部分组成．为了使正、负电子在测量区内不同位置进行对撞，在对撞测量区内设置两个方向相反的匀强磁场区域．对撞区域设计的简化原理如图所示：MN和PQ为足够长的竖直边界，水平边界EF将整个区域分成上下两部分，Ⅰ区域的磁场方向垂直纸面向内，Ⅱ区域的磁场方向垂直纸面向外，磁感应强度大小均为B．现有一对正、负电子以相同速率分别从注入口C和注入口D同时水平射入，在对撞测量区发生对撞．已知两注入口到EF的距离均为d，边界MN和PQ的间距为L，正电子的质量为m，电量为＋e，负电子的质量为m，电量为－e．

（1）试判断从注入口C入射的是正电子还是负电子；

（2）若L＝4d，要使正、负电子经过水平边界EF一次后对撞，求正电子在磁场中运动的时间；

（3）若只从注入口C射入电子，要使电子从D飞出，求电子射入的最小速率，及此时间距L的大小．

Answer 1

【答案】（1）负电子　（2）（3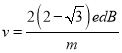）,L=4n（2－）d（其中n＝1,2,3，…）

【解析】

(1)由题意可知从注入口C入射时的应是负电子．

(2)电子运动轨迹如图中实线所示，由几何关系有

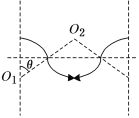
（R－d）2＋2＝R2

得

R＝2d

故

sin θ＝＝

得

θ＝

由

qvB＝m

得

T＝＝

由正、负电子运动的对称性知，正电子在磁场中运动的时间为

t＝2×T＝．

(3)能使电子从D点飞出的临界情况是第一次在Ⅱ区域中偏转的运动轨迹与MN相切，如图所示:

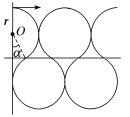
由几何关系知

α＝30°

且

r＋rcos α＝d

解得

r＝2（2－）d

由

qvB＝m

得

v＝

由图可知，

间距

L＝n×2r＝4n(2－)d（其中n＝1,2,3，…）．