题目内容
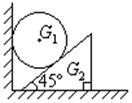
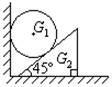
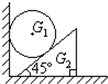 重量为G1的均匀球夹在光滑竖直平面和45°倾角的光滑斜块之间,如图所示,斜块重G2,斜块侧面与水平桌面间的摩擦系数为μ0(μ0<1),求:G1的最小值为多大时,才能使斜块滑动.(设最大静摩擦力等于滑动摩擦力)
重量为G1的均匀球夹在光滑竖直平面和45°倾角的光滑斜块之间,如图所示,斜块重G2,斜块侧面与水平桌面间的摩擦系数为μ0(μ0<1),求:G1的最小值为多大时,才能使斜块滑动.(设最大静摩擦力等于滑动摩擦力)
解:先对球进行受力分析,根据力的作用效果,重力分解为一个垂直于竖直挡板的分力N1,一个垂直斜面的分力N2,然后做平行四边形,如下图:
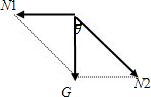
根据三角函数知识可求得球对斜面的压力为N2=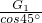 =
= G1
G1
然后对斜面进行受力分析,水平方向应该有:Ncos45°=μ0(G2+Nsin45°)
联立得:G1=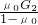
答:G1的最小值为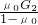 时,才能使斜面滑动.
时,才能使斜面滑动.
分析:先以G1为研究对象进行受力分析,表示出斜面对球的弹力,然后对斜面进行受力分析当球对斜面弹力在水平方向的分力与最大静摩擦力相等时是斜面滑动的临界条件.
点评:本题考查临界情况分析,熟练的应用隔离法进行受力分析和进行力的合成与分解是基础.

根据三角函数知识可求得球对斜面的压力为N2=
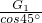 =
= G1
G1然后对斜面进行受力分析,水平方向应该有:Ncos45°=μ0(G2+Nsin45°)
联立得:G1=
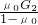
答:G1的最小值为
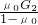 时,才能使斜面滑动.
时,才能使斜面滑动.分析:先以G1为研究对象进行受力分析,表示出斜面对球的弹力,然后对斜面进行受力分析当球对斜面弹力在水平方向的分力与最大静摩擦力相等时是斜面滑动的临界条件.
点评:本题考查临界情况分析,熟练的应用隔离法进行受力分析和进行力的合成与分解是基础.

练习册系列答案
相关题目
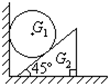 重量为G1的均匀球夹在光滑竖直平面和45°倾角的光滑斜块之间,如图所示,斜块重G2,斜块侧面与水平桌面间的摩擦系数为μ0(μ0<1),求:G1的最小值为多大时,才能使斜块滑动.(设最大静摩擦力等于滑动摩擦力)
重量为G1的均匀球夹在光滑竖直平面和45°倾角的光滑斜块之间,如图所示,斜块重G2,斜块侧面与水平桌面间的摩擦系数为μ0(μ0<1),求:G1的最小值为多大时,才能使斜块滑动.(设最大静摩擦力等于滑动摩擦力)