题目内容
如图,设在地面上方的真空室内,建立平面直角坐标系,在x<0的空间内有倾斜方向的匀强电场,电场强度为E1,在x=0.2m处有一与X轴垂直的荧光屏.一质量为m=4×10-7kg,带电量q=1×10-5C的带电粒子(重力不能忽略)从坐标为(-
m,0)处的A点由静止开始运动,它能沿x轴作直线运动,到达坐标原点O时的速度为v=1m/s.(g=10m/s2)
(1)求E1的大小和方向(方向角可用角的三角函数值表示)
(2)粒子打在荧光屏M点,求M点的坐标.
(3)若在x>0区域加竖直向上的匀强电场,场强E2=0.4N/C,且在如图平面内以坐标为(0.1m,0)的C点为圆心,半径为0.1m的圆形区域内有垂直于纸面的匀强磁场,粒子会打在荧光屏上坐标为(0.2m,0.1
m)的N点,求磁场的磁感应强度的大小和方向.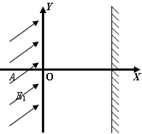
| 1 |
| 15 |
(1)求E1的大小和方向(方向角可用角的三角函数值表示)
(2)粒子打在荧光屏M点,求M点的坐标.
(3)若在x>0区域加竖直向上的匀强电场,场强E2=0.4N/C,且在如图平面内以坐标为(0.1m,0)的C点为圆心,半径为0.1m的圆形区域内有垂直于纸面的匀强磁场,粒子会打在荧光屏上坐标为(0.2m,0.1
| 3 |

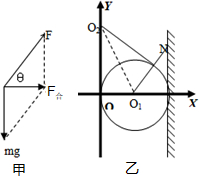
(1)粒子从A点到O点做匀加速直线运动,
位移为s=
| 1 |
| 15 |
由匀变速运动的速度位移公式可得:v2=2as,
解得:a=7.5m/s2;
由牛顿第二定律得:F合=ma=3×10-6N,
粒子受力如图甲所示,
由勾股定理可得:静电力F=5×10-6N,
电场强度E1=
| F |
| q |
(2)粒子到达O点后做平抛运动,粒子到达M点时,
在水平方向:x=vt=0.2m,竖直方向:y=
| 1 |
| 2 |
M点的坐标为(0.2m,-0.2m);
(3)静电力F2=qE2=4×10-4N,粒子重力G=mg=4×10-4N,
重力与电场力合力为零,粒子在磁场中做匀速圆周运动,
粒子离开磁场后做匀速直线运动,最后达到N点,
粒子打在N点,粒子进入磁场后沿顺时针方向做圆周运动,
由左手定则可知,磁场方向垂直于平面向里;
粒子运动轨迹如图乙所示,由几何知识可知,
圆周运动的半径r=0.1
| 3 |
粒子做圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m
| v2 |
| r |
解得:B=
| mv |
| qr |
答:(1)电场强度E1=
| F |
| q |
(2)M点的坐标为(0.2m,-0.2m);
(3)磁场的磁感应强度的大小为0.23T,方向:垂直于纸面向里.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
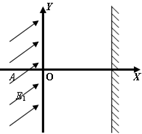 如图,设在地面上方的真空室内,建立平面直角坐标系,在x<0的空间内有倾斜方向的匀强电场,电场强度为E1,在x=0.2m处有一与X轴垂直的荧光屏.一质量为m=4×10-7kg,带电量q=1×10-5C的带电粒子(重力不能忽略)从坐标为(-
如图,设在地面上方的真空室内,建立平面直角坐标系,在x<0的空间内有倾斜方向的匀强电场,电场强度为E1,在x=0.2m处有一与X轴垂直的荧光屏.一质量为m=4×10-7kg,带电量q=1×10-5C的带电粒子(重力不能忽略)从坐标为(-

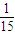 m,0)处的A点由静止开始运动,它能沿x轴作直线运动,到达坐标原点O时的速度为v=1m/s.(g=10m/s2)
m,0)处的A点由静止开始运动,它能沿x轴作直线运动,到达坐标原点O时的速度为v=1m/s.(g=10m/s2)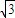 m)的N点,求磁场的磁感应强度的大小和方向.
m)的N点,求磁场的磁感应强度的大小和方向.