��Ŀ����
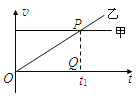
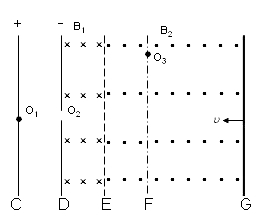
����Ŀ����ͼ��ʾ��C��DΪ��ƽ�н����壬C������磬D������磬E��FΪ������D�Ҳ�ų��е��������ߣ�C��D��E��F�������ƽ�С��������������d=10m������E�������ߵĴų������෴���Ÿ�Ӧǿ�ȴ�С��ΪB=1��10��2 T�����ڽ���������C��O1�ɾ�ֹ�ͷ�һ����m=1��0��10��12kg�������q=1��0��10��8C�Ĵ��������ӣ����ӱ��糡���ٺ�������D�е�С��O2����ų����ڴų����˶�ʱ��������F�ϵĵ�O3�������ڴų�����Բ���˶��İ뾶R=20m�����ӽ���ų���ȥ���ٵ糡����������������ȡ![]() ����
����
��1��C��D��ĵ�ѹU;
��2�����Ӵ�O2��O3����˶�ʱ��t��
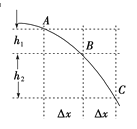
��3���������Ӵ���O2��ʼ���ҷ�������F��� 30m����һ��֮ƽ�еĵ���G���������ٶ�Ϊ0���ȼ���ֱ���˶�����������������ʱ�������˶�����ǡ���뵲��ƽ�У���ļ��ٶȴ�Сa��
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
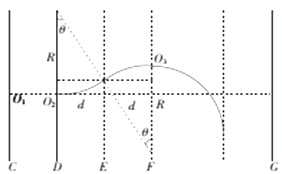
��������
�����������1�����ӽ���ų���������Բ���˶���![]()
���Ӵ�C�嵽D����ٹ��̣����ݶ��ܶ�����![]()
�������ݽ�ã�![]()
��2���ɼ��ι�ϵ�ɵã�![]()
��ã�![]()
������DE��EF֮����˶�ʱ���Ϊ![]() ,������O2��O3����˶�ʱ�䣺
,������O2��O3����˶�ʱ�䣺![]()
��![]()
�������ݽ�ã�![]()
��3�������˶�����ǡ���뵲��ƽ��ʱ�������˶�ʱ��:![]()
����G���ƶ�ʱ�䣺![]()
�ɼ��ι�ϵ֪��������G����������ʱ�������ƶ��ľ���Ϊ��![]()
����![]()
�������ݽ�ã�![]()

 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�