题目内容
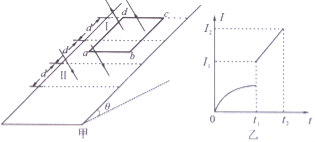
【题目】如图甲所示，倾角为
的光滑斜面上有两个宽度均为d的磁场区域I、Ⅱ，磁感应强度大小都为B，区域I的磁感应强度方向垂直斜面向上，区域Ⅱ的磁感应强度方向垂直斜面向下，两磁场区域间距为
d。斜面上有一矩形导体框，其质量为m，电阻为R，导体框ab、cd边长为，bc、ad边长为d。刚开始时，导体框cd边与磁场区域I的上边界重合；t=0时刻，静止释放导体框；t1时刻ab边恰进入磁场区域Ⅱ，框中电流为；随即平行斜面垂直于cd边对导体框施加力，使框中电流均匀增加，到t2时刻框中电流为I2。此时，ab边未出磁场区域Ⅱ，框中电流如图乙所示。求：
(1)在0~t2时间内，通过导体框截面的电荷量；
(2)在0-t1时间内，导体框产生的热量；
(3)在t1-t2时间内，导体框运动的加速度。
【答案】（1）
（2）
（3）
【解析】
试题分析：（1）由法拉第电磁感应定律、闭合电路欧姆定律和电流的定义，得0~t1阶段：
通过导体框截面的电量
由电流的定义，得t1~t2阶段：通过导体框截面的电量
0~t2阶段：通过导体框截面的电量
（2）设导体框t1时刻的速度为v1，在0~t1阶段：因
，可得：
根据动能定理可得：
联立可得：
导体框产生的热量等于克服安培力做功，即
（3）t1~t2阶段，因,由图可知I随时间均匀增加，
即：
解得：
练习册系列答案
华东师大版一课一练系列答案
相关题目
