题目内容
A、有A、B两球在光滑水平面上沿着一条直线运动,它们发生碰撞后粘在一起,已知碰前两球的动量分别为PA=20kg?m/s和PB=15kg?m/s,碰撞后B球的动量改变了△PB=-10kg?m/s,则碰撞后A球的动量为PA′= kg?m/s,碰撞前两球的速度大小之比vA:vB= .
B、一行星绕某恒星做圆周运动.由天文观测可得其运行的周期为T、线速度的大小为v,已知引力常量为G,则行星运动的轨道半径为 ,恒星的质量为 .
B、一行星绕某恒星做圆周运动.由天文观测可得其运行的周期为T、线速度的大小为v,已知引力常量为G,则行星运动的轨道半径为
分析:(A)AB球碰撞过程中动量守恒,根据动量守恒定律即可求解.
(B)根据圆周运动知识和已知物理量求出轨道半径.根据万有引力提供向心力,列出等式求出中心体的质量.
(B)根据圆周运动知识和已知物理量求出轨道半径.根据万有引力提供向心力,列出等式求出中心体的质量.
解答:解:(A)AB球碰撞过程中动量守恒,根据动量守恒定律得:
PA+PB=PA′+PB′
解得:PA′=30kgm/s
碰撞后速度相等,设此速度为v,则
mAv=30kgm/s
mBv=5kgm/s
解得:
=
碰撞前有:
mAvA=20kgm/s
mBvB=15kgm/s
解得:
=
(B)根据圆周运动知识得:
由v=
解得:r=
根据万有引力提供向心力,列出等式:
G
=m
解得:M=
故答案为:(A)30,2:9;(B)
;
PA+PB=PA′+PB′
解得:PA′=30kgm/s
碰撞后速度相等,设此速度为v,则
mAv=30kgm/s
mBv=5kgm/s
解得:
| mA |
| mB |
| 6 |
| 1 |
碰撞前有:
mAvA=20kgm/s
mBvB=15kgm/s
解得:
| vA |
| vB |
| 2 |
| 9 |
(B)根据圆周运动知识得:
由v=
| 2πr |
| T |
解得:r=
| vT |
| 2π |
根据万有引力提供向心力,列出等式:
G
| Mm |
| r2 |
| 4π2r |
| T2 |
解得:M=
| v3T |
| 2πG |
故答案为:(A)30,2:9;(B)
| vT |
| 2π |
| v3T |
| 2πG |
点评:(A)本题主要考查了动量守恒定律的直接应用,难度适中.
(B)本题考查万有引力与圆周运动问题.根据万有引力提供向心力,列出等式可求出中心体的质量,不能求出环绕体质量.
(B)本题考查万有引力与圆周运动问题.根据万有引力提供向心力,列出等式可求出中心体的质量,不能求出环绕体质量.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
(1)如图所示,用某单色光照射光电管的阴板K,会发生光电效应.在阳极A和阴极K之间加上反向电压,通过调节滑动变阻器的滑片逐渐增大加在光电管上的电压,直至电流表中电流恰为零,此时电压表的电压值U称为反向截止电压,现分别用频率为 和
和 的单色光照射阴极,测得反向截止电压分别为U1和U2.设电子的质量为m、电荷量为e,,下列说法正确的是 .(选对1个给3分,选对2个给4分,选对3个给6分,每选错1个扣3分,最低得分为0分)
的单色光照射阴极,测得反向截止电压分别为U1和U2.设电子的质量为m、电荷量为e,,下列说法正确的是 .(选对1个给3分,选对2个给4分,选对3个给6分,每选错1个扣3分,最低得分为0分)
A.频率为 的光照射时,光电子的最大初速度为 的光照射时,光电子的最大初速度为 |
B.频率为 的光照射时,光电子的最大初速度为 的光照射时,光电子的最大初速度为 |
C.阴极K金属的逸出功为 |
D.普朗克常数 |

(2)如图所示,A、B两球质量均为m,其间有压缩的轻短弹簧处于锁定状态(A、B两球与弹簧两端接触但不连接).弹簧的长度、两球的大小均忽略,整体视为质点,该装置从半径为R的竖直光滑圆轨道左侧与圆心等高处由静止下滑,滑至最低点时,解除对弹簧的锁定状态之后,B球恰好能到达轨道最高点,求:

①小球B解除锁定后的速度
②弹簧处于锁定状态时的弹性势能
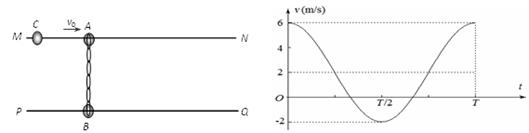
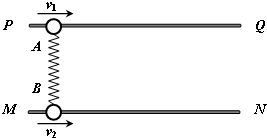 如图所示,PQ、MN是两根足够长且水平放置的固定光滑杆,杆上分别穿有质量分别为mA=2kg、mB=6kg的A、B两球(球可在杆上自由滑动),开始时用一轻质弹簧将A、B连接,弹簧刚好处于原长(如图).现突然分别给A、B施加一瞬时冲量,使二球同时获得v1=6m/s、v2=2m/s的初速度.则在以后的运动过程中(球未滑离杆),则下列说法正确的是( )
如图所示,PQ、MN是两根足够长且水平放置的固定光滑杆,杆上分别穿有质量分别为mA=2kg、mB=6kg的A、B两球(球可在杆上自由滑动),开始时用一轻质弹簧将A、B连接,弹簧刚好处于原长(如图).现突然分别给A、B施加一瞬时冲量,使二球同时获得v1=6m/s、v2=2m/s的初速度.则在以后的运动过程中(球未滑离杆),则下列说法正确的是( )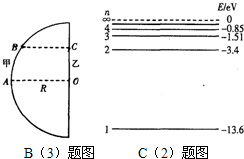 A.(选修模块3-3)
A.(选修模块3-3)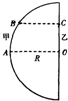 (3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?
(3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?