题目内容
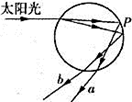
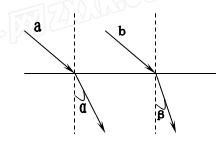
一束平行光线在垂直于玻璃半圆柱体轴线的平面内,按如图所示的方向射到半圆柱的平面上,已知光线与上表面的夹角为45°,求在半圆柱体的圆表面上有光线射出部分的弧长是多少?(已知玻璃半圆柱体的半径为0.2m,玻璃的折射率为 )
)
 )
)
解:设光线以45°射到半圆柱的平面上时的折射角为θ,如图所示。
所以由折射定律得: (1)2分
(1)2分
解得: ,即θ=30° (2)2分
,即θ=30° (2)2分
设从半圆柱体平面上的P、Q两点射入的光线,经折射后从玻璃中射向圆柱体圆表面上的A点和B点时的入射角恰好为临界角C,如图所示。
由于 得:C="arcsin"
得:C="arcsin"  =45° (3)2分
=45° (3)2分
所以由图及几何知识可求得:α=15°,β=75° (4)2分
由题意分析可知,在α=15°、β=75°,即α+β=90°所对应的圆柱体圆表面AB上有光线射出,且有光线射出部分的弧长AB= ×2πR=0.31m。 (5)2分
×2πR=0.31m。 (5)2分
所以由折射定律得:
 (1)2分
(1)2分解得:
 ,即θ=30° (2)2分
,即θ=30° (2)2分设从半圆柱体平面上的P、Q两点射入的光线,经折射后从玻璃中射向圆柱体圆表面上的A点和B点时的入射角恰好为临界角C,如图所示。
由于
 得:C="arcsin"
得:C="arcsin"  =45° (3)2分
=45° (3)2分所以由图及几何知识可求得:α=15°,β=75° (4)2分
由题意分析可知,在α=15°、β=75°,即α+β=90°所对应的圆柱体圆表面AB上有光线射出,且有光线射出部分的弧长AB=
 ×2πR=0.31m。 (5)2分
×2πR=0.31m。 (5)2分略

练习册系列答案
相关题目

 的方向入射到
的方向入射到 面上,光从
面上,光从 面射出,在图示出射光线中(光线②平行于
面射出,在图示出射光线中(光线②平行于

 =45
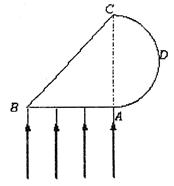
=45 , ADC为一圆弧,其圆心在AC边的中点,此透明物体的折射率为n=2.0.若一束宽度与AB边长度相等的平行光从AB边垂直射入透明物体,试由光路图画出光线从ADC圆弧射出的区域,并求此区域的圆弧长度s.(不考虑经ADC圆弧反射后的光线)
, ADC为一圆弧,其圆心在AC边的中点,此透明物体的折射率为n=2.0.若一束宽度与AB边长度相等的平行光从AB边垂直射入透明物体,试由光路图画出光线从ADC圆弧射出的区域,并求此区域的圆弧长度s.(不考虑经ADC圆弧反射后的光线)