��Ŀ����
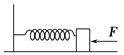
����Ŀ����ͼ��ʾ��ԭ���ֱ�ΪL1��L2������ϵ���ֱ�Ϊk1��k2�����ʵ�����ֱ�������컨���ϣ�������֮����һ����Ϊm1�����壬���¶˹�������Ϊm2����һ���壬����װ�ô��ھ�ֹ״̬��
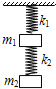
��1����ʱ�������ɵ��ܳ���Ϊ���
��2������һ������ΪM��ƽ��������������ֱ��������������ֱ���������ɵ��ܳ��ȵ��������ɵ�ԭ��֮�ͣ�����ʱƽ���ܵ���������m2��ѹ����
���𰸡���1��L1+L2+![]() +
+![]() ��2��
��2��![]()
����������1������ϵ��Ϊk1���ʵ����ܵ�������������m1+m2��g���������쳤��Ϊx1�����ݺ��˶����У�
��m1+m2��g=k1x1
��ã�x1=![]()
����ϵ��Ϊk2���ʵ����ܵ�����������m2g���������쳤��Ϊx2�����ݺ��˶����У�
m2g=k2x2
��ã�x2=![]()
��ʱ�������ɵ��ܳ���Ϊ��L=L1+L2+x1+x2=L1+L2+![]() +
+![]()
��2����һ��ƽ��������������ֱ��������������ֱ���������ɵ��ܳ��ȵ��������ɵ�ԭ��֮��ʱ������ĵ���Ӧ��ѹ��x������ĵ��ɱ�����x
��m1Ϊ������ƽ���ϵ��
��k1+k2��x=m1g
��ã�x=![]()
��m2Ϊ������ƽ���m2��֧����ΪFN������ƽ���ϵ��
FN=k2x+m2g=k2��![]() +m2g=
+m2g=![]() +m2g=
+m2g=![]()
����ʱƽ���ܵ���������m2��ѹ��FN'=![]()