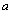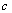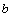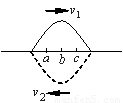题目内容
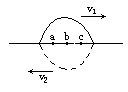
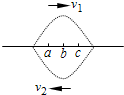 一根水平的弹性细绳上,一上一下两个形状相同的正弦半波相向传播,某个时刻恰好完全叠合,如图.a、b、c是细绳上三个质点,且b是此刻波的正中点,则( )
一根水平的弹性细绳上,一上一下两个形状相同的正弦半波相向传播,某个时刻恰好完全叠合,如图.a、b、c是细绳上三个质点,且b是此刻波的正中点,则( )分析:波的叠加中,质点的实际位移等于各个波单独传播时引起位移的矢量和;采用微平移法判断质点的振动情况.
解答:解:A、B、波的叠加中,波形单独传播,不受影响,质点的实际位移等于各个波单独传播时引起位移的矢量和,故此刻a、b、c的位移均为零;
经过很短的△t时间,a的位移为负、b的位移为零、c的位移为正,故a的速度向下、b的速度为零、c的速度向上;
故A错误,B正确;
C、b点速度为零,会持续一小段时间,故加速度为零,最小,故C错误;
D、c质点此刻合运动的速度方向向上,故D错误;
故选B.
经过很短的△t时间,a的位移为负、b的位移为零、c的位移为正,故a的速度向下、b的速度为零、c的速度向上;
故A错误,B正确;
C、b点速度为零,会持续一小段时间,故加速度为零,最小,故C错误;
D、c质点此刻合运动的速度方向向上,故D错误;
故选B.
点评:本题关键是明确波的叠加原理,知道质点的死实际位移等于各个波单独传播时引起位移的矢量和,基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目