题目内容
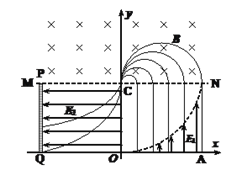
【题目】如图,在xOy坐标平面第一象限内![]() 的范围中,存在以
的范围中,存在以![]() 为上边界的沿y轴正方向的匀强电场,场强大小E1=2.0×102N/C.在直线MN(方程为y=1m)的上方存在方向垂直纸面向里、磁感应强度为B的匀强磁场.在x=-1m处有一与y轴平行的接收板PQ,板两端分别位于MN直线和x轴上;在第二象限,MN和PQ围成的区域内存在沿x轴负方向的匀强电场,场强大小为E2.现有大量带正电的粒子从x轴上0<x<lm的范围内同时由静止释放,粒子的比荷均为
为上边界的沿y轴正方向的匀强电场,场强大小E1=2.0×102N/C.在直线MN(方程为y=1m)的上方存在方向垂直纸面向里、磁感应强度为B的匀强磁场.在x=-1m处有一与y轴平行的接收板PQ,板两端分别位于MN直线和x轴上;在第二象限,MN和PQ围成的区域内存在沿x轴负方向的匀强电场,场强大小为E2.现有大量带正电的粒子从x轴上0<x<lm的范围内同时由静止释放,粒子的比荷均为![]() ,不计粒子的重力及其相互作用.
,不计粒子的重力及其相互作用.

(1)求在x=0.5m处释放的粒子射出电场E1时的速度大小;
(2)若进入磁场的所有带电粒子均从MN上同一点离开磁场,求磁感应强度B的大小;
(3)若在第(2)问情况下所有带电粒子均被PQ板接收,求电场强度E2的最小值和在E2最小的情况下最先打在接收板上的粒子运动的总时间.(可用分数表示)
【答案】(1) 4×103m/s (2) B=0.1T (3)![]()
【解析】(1)由题意得,于x处释放的粒子在电场中加速的位移为y,且满足y=x2①
设射出电场E1时的速度大小为v,由动能定理可得![]() ②
②
由①②式可得:![]() ③
③
代入x=0.5m可得:v0.5=4×103m/s
(2)粒子进入磁场后做匀速圆周运动,设半径为r,由牛顿第二定律可得:
![]() ④
④
由③④式解得:![]() ⑤
⑤
由⑤式可得,当磁感应强度B一定时,轨道半径r与x成正比,当x趋近于零时时,粒子做圆周运动的轨道半径趋近于零,即所有粒子经磁场偏转后都从C点射出磁场,且有
2r=x⑥
由⑤⑥式可得B=0.1T
(3)粒子从C点沿y轴负方向进入电场强度大小为E2的范围后,都在电场力作用下做类平抛运动,若所有带电粒子均被PQ板接收,则从x=1m处出发的粒子刚好运动到Q点,对应电场强度E2的最小值E2min,设该粒子在场强大小为E2min的电场中运动的初速度为v1,时间为t3,加速度为a2,有:y=v1t3⑦
![]() ⑧
⑧
![]() ⑨
⑨
将y=1m,x=1m代入③⑦⑧⑨两式可得E2min=8.0×102 N/C
由题意得,在E2最小的情况下最先打在接收板上的粒子为从x=1m处出发的粒子,设该粒子在场强大小为E1的电场中运动的时间为t1,在磁场中运动的时间为t2,则有:![]() ⑩
⑩
在匀强磁场中转过θ=π的圆心角,有πr=v1t2 ⑾
故该粒子所经历的总时间t=t1+t2+t3 ⑿
可得:![]()