题目内容
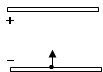 真空中水平放置两带电的金属板,相距为d.一个质量为m、带电量为+q的粒子,从负极板中央以速度v0垂直极板射入电场.当板间电压为U时,粒子经
真空中水平放置两带电的金属板,相距为d.一个质量为m、带电量为+q的粒子,从负极板中央以速度v0垂直极板射入电场.当板间电压为U时,粒子经| d |
| 4 |
分析:根据动能定理,结合电场强度的变化和动能的变化量,求出运动位移的变化量,从而进行判断.
解答:解:A、以速度v0垂直极板射入电场.当板间电压为U时,粒子经
的距离就要返回,根据动能定理知,-qE
=0-
mv02,若将初速度增大1倍,则初动能变为原来的4倍,根据动能定理知,粒子一直运动上级板速度才减为零.故A错误.
B、根据动能定理知,-qEs=0-
mv02,使板间的电压减半,电场强度变为原来的
,运动位移变为原来的2倍,即粒子走到板的中央才返回.故B正确.
C、根据动能定理知,-qEs=0-
mv02,v0和U同时减半,初动能变为原来的
,电场强度变为原来的
,则运动的位移变为原来的
,即
d.故C错误.
D、根据动能定理知,-qEs=0-
mv02,初速度增大为原来的2倍,则初动能变为原来的4倍,两板间距离变为原来的2倍,电场强度变为原来的
,则运动的位移变为原来8倍,即2d,则粒子一直运动到上级板速度才减为零.故D错误.
故选:B.
| d |
| 4 |
| d |
| 4 |
| 1 |
| 2 |
B、根据动能定理知,-qEs=0-
| 1 |
| 2 |
| 1 |
| 2 |
C、根据动能定理知,-qEs=0-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
D、根据动能定理知,-qEs=0-
| 1 |
| 2 |
| 1 |
| 2 |
故选:B.
点评:解决本题的关键抓住粒子动能的变化量,结合电场力的变化,运用动能定理进行求解.

练习册系列答案
相关题目
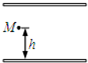 如图所示,在真空中水平放置的平行板电容器两板间的电压为U1=200V,在距下板h=1.6cm的M点,带负电的液滴处于静止状态.如果使两板之间电压突然减小到U2=100V,取g=10m/s2.则带电液滴运动到极板上需要经历的时间t为多少?
如图所示,在真空中水平放置的平行板电容器两板间的电压为U1=200V,在距下板h=1.6cm的M点,带负电的液滴处于静止状态.如果使两板之间电压突然减小到U2=100V,取g=10m/s2.则带电液滴运动到极板上需要经历的时间t为多少? (2009?天津)如图所示,带等量异号电荷的两平行金属板在真空中水平放置,M、N为板间同一电场线上的两点,一带电粒子(不计重力)以速度vM经过M点在电场线上向下运动,且未与下板接触,一段时间后,粒子以速度vN折回N点.则( )
(2009?天津)如图所示,带等量异号电荷的两平行金属板在真空中水平放置,M、N为板间同一电场线上的两点,一带电粒子(不计重力)以速度vM经过M点在电场线上向下运动,且未与下板接触,一段时间后,粒子以速度vN折回N点.则( )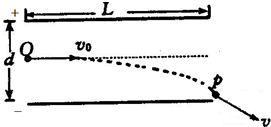 如图所示,在真空中水平放置一对金属板.在两板间加以电压U=800V,板间距离为d=2cm,板长L=10cm.一电荷量为q=1×10-9C质量为m=5×10-6kg的带电粒子从极板中央以水平速度v0=2m/s射入电场.试分析带电粒子在电场中的运动情况.(不计粒子的重力)
如图所示,在真空中水平放置一对金属板.在两板间加以电压U=800V,板间距离为d=2cm,板长L=10cm.一电荷量为q=1×10-9C质量为m=5×10-6kg的带电粒子从极板中央以水平速度v0=2m/s射入电场.试分析带电粒子在电场中的运动情况.(不计粒子的重力)