题目内容
11．
如图，质量为m的小球用轻绳悬挂在O点，在水平恒力F=mgtanθ作用下，小球从静止开始由A经B向C运动．则小球（ ）| A． | 先加速后减速 | B． | 在B点加速度为零 | ||
| C． | 在C点速度为零 | D． | 在C点加速度为gtanθ |
分析 根据动能定理求出小球速度为零时细线与竖直方向的角度，得出小球在整个过程中的运动规律．在C点，抓住径向的合力为零，通过数学知识，结合受力求出合力的大小，从而求出C点的加速度．
解答 解：设小球摆到的最大角度为α，根据动能定理得，FLsinα-mgL（1-cosα）=0，又F=mgtanθ
解得α=2θ，即在C点的速度为零．可知小球先加速后减速，故A、C正确．
在B点，小球的速度不为零，则向心加速度不为零，所以加速度不为零，故B错误．
在C点，速度为零，小球受重力和拉力，垂直绳子方向的合力为零，则小球所受的合力为mgsin2θ-mgtanθcos2θ=mgtanθ，则C点的加速度为gtanθ，故D正确．
故选：ACD．
点评 本题考查了牛顿第二定律和动能定理的基本运用，知道小球速度为零时，径向的合力为零，本题对数学三角函数要求较高，需加强这方面的训练．
练习册系列答案
活力课时同步练习册系列答案
相关题目
1．下列是教材中的四副插图中，关于下列四幅图片所涉及的物理思想、物理方法、物理实验、物理假设，说法不正确的是（ ）
| A． |  此图是伽利略研究自由落体运动时用以“冲淡”重力而使得时间容易测量采用的一种巧妙方法 | |
| B． |  此图中小球从A斜面滑下，它要滑上B斜面的等高处，无论B斜面倾角多大，它总是记得自己的起始高度，这是伽利略研究守恒量时采用的方法 | |
| C． |  利用此图可以探究感应电流方向，图中小磁铁无论向上运动还是向下运动，电流表中指针偏转方向都相同 | |
| D． |  此图是一种延迟继电器的示意图，即使图中B线圈断开，也不会影响继电器的延迟效果 |
2．有一个铜环和一个木环，它们的形状、尺寸相同．用两块同样的条形磁铁以同样的速度，将N极垂直圆环平面分别插入铜环和木环中，则同一时刻这两环的磁通是（ ）
| A． | 铜环磁通大 | B． | 木环磁通大 | ||
| C． | 两环磁通一样大 | D． | 两环磁通无法比较 |
19．铀核可以发生衰变和裂变，铀核的（ ）
| A． | 衰变和裂变都能自发发生 | |
| B． | 衰变和裂变都不能自发发生 | |
| C． | 衰变能自发发生而裂变不能自发发生 | |
| D． | 衰变不能自发发生而裂变能自发发生 |
6．重离子肿瘤治疗装置中的回旋加速器可发射+5价重离子束，其束流强度为1.2×10-5A，则在1s内发射的重离子个数为（e=1.6×10-19C）（ ）
| A． | 3.0×1012 | B． | 1.5×1013 | C． | 7.5×1013 | D． | 3.75×1014 |
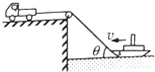如图，汽车在平直路面上匀速运动，用跨过光滑定滑轮的轻绳牵引轮船，汽车与滑轮间的绳保持水平，当牵引轮船的绳与水平方向成θ角时，轮船速度为v，绳的拉力对船做功的功率为P，此时绳对船的拉力为$\frac{P}{vcosθ}$．若汽车还受到恒定阻力f，则汽车发动机的输出功率为fvcosθ+P．
如图所示，质量m=2.0kg的物体以初速度v0=5.0m/s水平向右滑上逆时针匀速转动的传送带左端．传送带右端与平台MN平滑相连．平台左侧部分MP区域宽度S，物体通过此区域时将额外受到一水平向左、大小为12N的恒力F．已知传送带长度L=2.25m，物体与传送带、平台MN见的动摩擦因数均为0.2，g=10m/s2．求：
17．
如图所示是一半径为R的玻璃球体，0为球心，AB为水平直径，M点是玻璃球的最高点，来自B点的光线BD从D点射出，出射光线平行于AB，已知∠ABD=30°，光在真空中的传播速度为c，则（ ）
如图所示是一半径为R的玻璃球体，0为球心，AB为水平直径，M点是玻璃球的最高点，来自B点的光线BD从D点射出，出射光线平行于AB，已知∠ABD=30°，光在真空中的传播速度为c，则（ ）| A． | 此玻璃的折射率为$\frac{2}{3}$$\sqrt{3}$ | |
| B． | 光线从B传到D的时间为$\frac{3R}{c}$ | |
| C． | 若增大∠ABD，光线不可能在DM段发生全反射现象 | |
| D． | 若减小∠ABD，从AD段射出的光线均平行于AB |
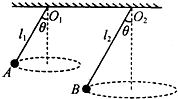如图所示，两个相同的小球A、B用长度分别为l1、l2的细线悬挂在天花板的O1，O2点，两球在水平面内做匀速圆周运动，两根细线与竖直轴夹角均为θ．设A，B两球的线速度分别为vA、vB，角速度分别为ωA、ωB，加速度分别为aA、aB，两根细线的拉力分别为FA、FB，则（ ）