题目内容
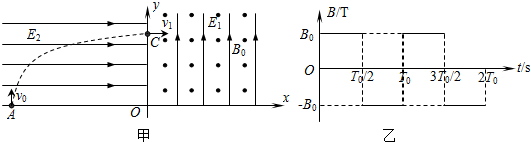
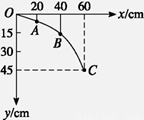
在竖直平面内建立一平面直角坐标系xoy,x轴沿水平方向,如图甲所示.坐标系的第一象限内有一正交的匀强电场和匀强磁场,电场方向竖直向上,场强为E1,磁场方向垂直纸面,磁感应强度B0=
,方向按图乙所示规律变化(以垂直纸面向外的磁场方向为正向),第二象限内有一水平向右的匀强电场,场强E2=2E1.一个比荷
=102C/kg的带正电的粒子(可视为质点)以v0=4m/s的速度在-x上的A点竖直向上抛出,恰能以v1=8m/s速度从+y上的C点水平进入第一象限.取粒子刚进入第一象限时t=0,g=10m/s2,试求:
(1)AC间电势差UAC.
(2)为确保粒子不再越过OC进入第二象限,则交变磁场周期最大值Tm为多少?若磁场周期为上述最大值,粒子打到+x上D点(图中未标出),此时OD长L0为多少?
3+
| ||
| 10 |
| q |
| m |

(1)AC间电势差UAC.
(2)为确保粒子不再越过OC进入第二象限,则交变磁场周期最大值Tm为多少?若磁场周期为上述最大值,粒子打到+x上D点(图中未标出),此时OD长L0为多少?
分析:(1)将粒子在第二象限内的运动分解为水平方向和竖直方向,得出两个方向上的运动规律,结合运动学公式和牛顿第二定律求出带电微粒运动到C点的纵坐标值h及电场强度E1,从而可求得AC间电势差;
(2)当交变磁场周期取最大值而粒子不再越过y轴时,根据几何关系求出Tm和L0
(2)当交变磁场周期取最大值而粒子不再越过y轴时,根据几何关系求出Tm和L0
解答:解:(1)设OC高为h,OA长为L,粒子在第一象限运动时间为t1,则
-mgh=0-
m
qE1L=
m
L=
v1t1,h=
v0t1
代入数据可得:h=0.8m,L=1.6m,E1=0.2V/m,
所以UAC=E1L=0.32V
(2)粒子在第一象限运动时因mg-qE1=0,
故粒子做匀速圆周运动运动,设粒子运动圆轨道半径为R,周期为T.
则qv1B0=
可得R=
m,即R=
由匀速圆周运动的周期T=
,代入B0得:
T=
s
当交变磁场周期取最大值而粒子不进入第一象限时可作如图运动情形:
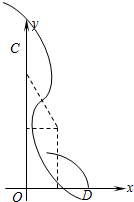
由图可知T0=
T=
s
L0=2R=
m
答:(1)AC间电势差为0.32V.
(2)交变磁场周期最大值为
s; OD长
m
-mgh=0-
| 1 |
| 2 |
| v | 2 0 |
qE1L=
| 1 |
| 2 |
| v | 2 1 |
L=
| 1 |
| 2 |
| 1 |
| 2 |
代入数据可得:h=0.8m,L=1.6m,E1=0.2V/m,
所以UAC=E1L=0.32V
(2)粒子在第一象限运动时因mg-qE1=0,
故粒子做匀速圆周运动运动,设粒子运动圆轨道半径为R,周期为T.
则qv1B0=
m
| ||
| R |
可得R=
| 0.8 | ||
3+
|
| h | ||
3+
|
由匀速圆周运动的周期T=
| 2πm |
| qB0 |
T=
π(3-
| ||
| 30 |
当交变磁场周期取最大值而粒子不进入第一象限时可作如图运动情形:

由图可知T0=
| 5 |
| 6 |
(3-
| ||
| 36 |
L0=2R=
4(3-
| ||
| 15 |
答:(1)AC间电势差为0.32V.
(2)交变磁场周期最大值为
(3-
| ||
| 36 |
4(3-
| ||
| 15 |
点评:本题中质点在复合场运动,分析受力情况,确定质点的运动情况是解题的基础.结合粒子运动的周期性以及临界状态,运用数学几何知识综合求解.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
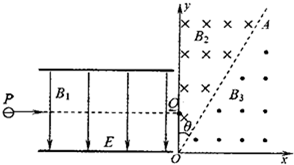 如图所示,水平放置的两平行金属板间存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度为B1,方向与纸面垂直,电场的场强E=2.0×105V/m,方向竖直向下,PQ为板间中线.紧靠平行板右侧边缘建立平面直角坐标系xOy,在第一象限内,存在着以AO为理想边界的两个匀强磁场区域,方向如图所示,磁感应强度B2=B3=0.6T,AO和y轴间的夹角θ=30°.一束带负电的粒子,质量不同,带电量q=2.5×10-8C,以v=5×105m/s的水平速度从P点射入板间,沿PQ做直线运动,穿出平行板区域后从y轴上坐标为(0,0.3m)的Q点垂直于y轴射入磁场区域.(粒子的重力不计)
如图所示,水平放置的两平行金属板间存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度为B1,方向与纸面垂直,电场的场强E=2.0×105V/m,方向竖直向下,PQ为板间中线.紧靠平行板右侧边缘建立平面直角坐标系xOy,在第一象限内,存在着以AO为理想边界的两个匀强磁场区域,方向如图所示,磁感应强度B2=B3=0.6T,AO和y轴间的夹角θ=30°.一束带负电的粒子,质量不同,带电量q=2.5×10-8C,以v=5×105m/s的水平速度从P点射入板间,沿PQ做直线运动,穿出平行板区域后从y轴上坐标为(0,0.3m)的Q点垂直于y轴射入磁场区域.(粒子的重力不计)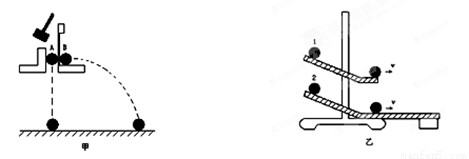


 如下图所示,两平行金属板间存在相互平行的匀强磁场和匀强电场,电场强度为E,磁感强度为B,方向都在竖直平面内与金属板相垂直.平行板右侧有一荧光屏MN在竖直平面内与金属板相垂直.荧光屏MN中心为O,O'是电、磁场上边缘的一点,连线OO'垂直荧光屏MN,其长度为L,在荧光屏MN上建立一直角坐标系,原点为O,y轴向上,x轴垂直纸面向外,一束具有相同速度和荷质比的带电粒子,沿OO'方向由O射入此电、磁场中,最后打在荧光屏上,屏上亮点坐标为
如下图所示,两平行金属板间存在相互平行的匀强磁场和匀强电场,电场强度为E,磁感强度为B,方向都在竖直平面内与金属板相垂直.平行板右侧有一荧光屏MN在竖直平面内与金属板相垂直.荧光屏MN中心为O,O'是电、磁场上边缘的一点,连线OO'垂直荧光屏MN,其长度为L,在荧光屏MN上建立一直角坐标系,原点为O,y轴向上,x轴垂直纸面向外,一束具有相同速度和荷质比的带电粒子,沿OO'方向由O射入此电、磁场中,最后打在荧光屏上,屏上亮点坐标为