题目内容
8. 如图所示,在光滑的水平面上静止着一个质量为4m的木板B,B的左端静止着一个质量为2m的物块A,已知A,B之间的动摩擦因数为μ,现有质量为m的小球以水平速度v0飞来与物块A发生弹性碰撞,在整个过程中物块A始终未滑离木板B,且物块A可视为质点,求:
如图所示,在光滑的水平面上静止着一个质量为4m的木板B,B的左端静止着一个质量为2m的物块A,已知A,B之间的动摩擦因数为μ,现有质量为m的小球以水平速度v0飞来与物块A发生弹性碰撞,在整个过程中物块A始终未滑离木板B,且物块A可视为质点,求:(1)到物块A相对B静止时,物块A的位移;
(2)木板B至少多长?
分析 (1)小球与A碰撞过程动量守恒、机械能守恒,应用动量守恒定律与机械能守恒定律可以求出碰撞后A的速度,A、B系统动量守恒,应用运动学公式求出A的位移.
(2)应用运动学公式求出B的位移,然后求出B的最小长度,或应用能量守恒定律求出B的长度.
解答 解:(1)小球与A发生弹性碰撞,碰撞过程系统动量与机械能守恒,
以向右为正方向,由动量守恒定律得:mv0=mv1+2mvA,
由机械能守恒定律得:$\frac{1}{2}$mv02=$\frac{1}{2}$mv12+$\frac{1}{2}$•2mvA2,解得:vA=$\frac{2}{3}$v0,v1=-$\frac{1}{3}$v0;
A、B系统动量守恒,以向右为正方向,
由动量守恒定律得:2mvA=(2m+4m)v,解得:v=$\frac{2}{9}$v0,
A做匀减速直线运动,由速度位移公式得:
v2-vA2=2(-μg)xA,解得:xA=$\frac{16{v}_{0}^{2}}{81μg}$;
(2)B做初速度为零的匀加速直线运动,
B的加速度:a′=$\frac{μ•2mg}{4m}$=$\frac{1}{2}$μg,
由匀变速直线运动的速度位移公式得:
v2=2a′xB,解得:xB=$\frac{4{v}_{0}^{2}}{81μg}$,
B的长度至少为:L=xA-xB=$\frac{4{v}_{0}^{2}}{27μg}$;
答:(1)到物块A相对B静止时,物块A的位移为$\frac{16{v}_{0}^{2}}{81μg}$;
(2)木板B至少长为$\frac{4{v}_{0}^{2}}{27μg}$.
点评 本题考查了求位移与木板长度问题,考查了动量守恒定律的应用,分析清楚物体运动过程是解题的关键,应用动量守恒定律、运动学公式可以解题.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | 甲、乙两车之间的距离一定不断减小 | |
| B. | 甲、乙两车之间的距离一定不断增大 | |
| C. | 若v>$\sqrt{2{a}_{1}+{a}_{2}d}$,则两车一定不会相撞 | |
| D. | 若v<$\sqrt{2({a}_{1}+{a}_{2})d}$,则两车一定不会相撞 |
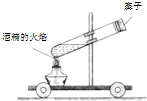
| A. | 由于塞子的质量小于小车质量,喷出时塞子受到的冲击力将大于小车受到的冲击力 | |
| B. | 由于塞子的质量小于小车质量,喷出时塞子受到的冲击力将小于小车受到的冲击力 | |
| C. | 塞子喷出瞬间小车对水平面的压力大于小车自身的重力 | |
| D. | 若增大试管内水的质量则可以增大小车的速度 |
| A. | 0N | B. | 5N | C. | 20N | D. | 80N |
| A. | 从I=$\frac{U}{R}$可知,导体中的电流跟加在它两端的电压成正比,跟它的电阻成反比 | |
| B. | 从 R=$\frac{U}{I}$ 可知,导体的电阻跟导体两端的电压成正比,跟导体中的电流成反比 | |
| C. | 从 U=IR 可知,导体两端的电压随电阻的增大而增大 | |
| D. | 从 R=$\frac{U}{I}$可知,导体两端的电压为零时,导体的电阻也为零 |
| A. | 20km/h | B. | 30km/h | C. | 35km/h | D. | 40km/h |