题目内容
如图甲所示，两根相距L=0.5m且足够长的固定金属直角导轨，一部分水平，另一部分竖直。质量均为m=0.5kg的金属细杆ab、cd始终与导轨垂直且接触良好形成闭合回路，水平导轨与ab杆之间的动摩擦因数为μ，竖直导轨光滑。ab与cd之间用一根足够长的绝缘细线跨过定滑轮相连，每根杆的电阻均为R=1Ω，其他电阻不计。整个装置处于竖直向上的匀强磁场中，现用一平行于水平导轨的恒定拉力F作用于ab杆，使之从静止开始向右运动，ab杆最终将做匀速运动，且在运动过程中，cd杆始终在竖直导轨上运动。当改变拉力F的大小时，ab杆相对应的匀速运动的速度v大小也随之改变，F与v的关系图线如图乙所示。不计细线与滑轮之间的摩擦和空气阻力，g取10m/s2。求：（1）杆与水平道轨之间的动摩擦因数μ和磁感应强度B各为多大？
（2）若ab杆在F=9N的恒力作用下从静止开始向右运动8m时达到匀速状态，则在这一过程中整个回路产生的焦耳热为多少？
解：设ab杆匀速运动时的速度为v，则回路中产生的感应电动势 
① 回路中的感应电流
② ab杆所受到的安培力
③ 以T表示细线的拉力，对ab杆，由平衡条件得
④ 对cd杆，有
⑤ 联立③④⑤解得
⑥ 由图乙可知：当
时，
；当
时，
代入⑥解得：
，
⑦ （2）ab杆从静止开始向右运动直到匀速运动的过程中，设回路产生的焦耳热为Q，对ab、cd组成的系统，由能量守恒定律可得
⑧ 解得：
⑨
① 回路中的感应电流 ② ab杆所受到的安培力 ③ 以T表示细线的拉力，对ab杆，由平衡条件得 ④ 对cd杆，有 ⑤ 联立③④⑤解得 ⑥ 由图乙可知：当时，；当时，代入⑥解得：， ⑦ （2）ab杆从静止开始向右运动直到匀速运动的过程中，设回路产生的焦耳热为Q，对ab、cd组成的系统，由能量守恒定律可得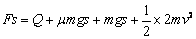 ⑧ 解得： ⑨ 
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
