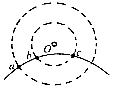��Ŀ����
����Ŀ����ͼ��ʾ�����ABC�� ��AB��Ϊһ�뾶R=0.2m�Ĺ⻬ ![]() Բ�ι����BC��Ϊ�㹻���Ĵֲ�ˮƽ�森һ����Ϊ0.1kg��С����P��A��Ӿ�ֹ��ʼ�»�������B��ʱ�뾲ֹ��B����һ����Ϊ0.1kg��С����Q��ײ��ճ��һ����������BCˮƽ���ϻ���0.5m��ͣ�£���gȡ10m/s2������
Բ�ι����BC��Ϊ�㹻���Ĵֲ�ˮƽ�森һ����Ϊ0.1kg��С����P��A��Ӿ�ֹ��ʼ�»�������B��ʱ�뾲ֹ��B����һ����Ϊ0.1kg��С����Q��ײ��ճ��һ����������BCˮƽ���ϻ���0.5m��ͣ�£���gȡ10m/s2������
��1��С����P�յ���Բ�ι��B ��ʱ�����������֧����FN�Ĵ�С��
��2��С����P��С����Q��ײ��ͬ�˶����ٶ�v����С��
��3��������ˮƽ���Ķ�Ħ�������̵Ĵ�С��
���𰸡�
��1���⣺С����P�ع⻬Բ�ι���»�����Բ�ι����B�Ĺ����У���е���غ㣬�ɻ�е���غ㶨�ɵã�
![]() ��
��
��B�㣬��ţ�ٵڶ����ɵã� ![]() ��
��
�������ݽ�ã�FN=3N��vB=2m/s��
��С����P�յ���Բ�ι��B��ʱ�����������֧����FN�Ĵ�СΪ3N��
��2���⣺С����P��С����Q��B����ײ���٣���ײ�����ж����غ㣬��P���ٶȷ���Ϊ�������ɶ����غ㶨�ɵã�
mvB=2mv����
�������ݽ�ã�v��=1m/s��
��С����P��С����Q��ײ��ͬ�˶����ٶ�v����СΪ1m/s��
��3���⣺������ˮƽ���ϻ��еĹ����У��ܵ�����Ħ���������ã��ɶ��ܶ����ã�
����2mgs=0�� ![]() mv��2��
mv��2��
�������ݽ�ã���= ![]() =0.1��
=0.1��
�𣺻�����ˮƽ���Ķ�Ħ�������̵Ĵ�СΪ0.1��
����������1���ɻ�е���غ㶨�ɿ���������鵽��B��ʱ���ٶȣ���ţ�ٵڶ����ɿ������֧��������2���ɶ����غ㶨�ɿ��������ͬ�ٶȣ���3���ɶ��ܶ������������Ħ��������
�����㾫����������Ҫ�������������Ͷ��ܶ������ۺ�Ӧ�õ����֪ʶ�㣬��Ҫ��������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ����������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݲ�����ȷ�����⣮