��Ŀ����
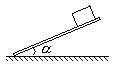
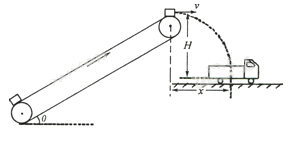
����Ŀ����ͼ�����ô��ʹ�װ��ú���ʾ��ͼ�����У����ʹ��ĴӶ�����������Բ��֮��ľ���Ϊs=3m�����ʹ���ˮƽ�����ļн���=37����ú���봫�ʹ���Ķ�Ħ��������=0.8�����ʹ��������ֺʹӶ��ְ뾶��ȣ��������ᶥ������ú���װ�����ֱ�߶�H =" 1.8" m ������ú���������ĵ�ˮƽ����x = 0.6m�����ڴ��ʹ����ɾ�ֹ�ͷ�һú�飨����Ϊ�ʵ㣩��ú��ǡ�����ֵ���ߵ�ˮƽ�׳������ڳ������ģ�ȡg =" 10" m/s2��sin37��="0.6," cos37��= 0.8����
��l�������ֵİ뾶��
��2�����ʹ������˶����ٶȣ�
��3��ú���ڴ��ʹ���ֱ�߲����˶���ʱ�䡣
���𰸡���1��0.1m��2��1m/s����3��4.25s
�������������������1��Ҫʹú�����ֵ���ߵ���ƽ���˶�����ú�鵽���ֵ���ߵ�ʱ���ֵ�ѹ��Ϊ�㣬����ƽ���˶��Ĺ�������뿪���ʹ���ߵ���ٶȣ����ţ�ٵڶ���������뾶�Ĵ�С��
��2������ţ�ٵڶ����ɣ�����˶�ѧ��ʽȷ�����ʹ����ٶȣ�
��3��ú���ڴ��ʹ��������ȼ����˶��������˶��������˶�ѧ��ʽ�ֱ��������ʱ�䣬�Ӷ��ó�ú���ڴ��ʹ���ֱ�߲����˶���ʱ�䣮
�⣺��1����ƽ���˶��Ĺ�ʽ����x=vt��![]()
�������ݽ�� v=1m/s
Ҫʹú�����ֵ���ߵ���ƽ���˶�����ú�鵽���ֵ���ߵ�ʱ���ֵ�ѹ��Ϊ�㣬
��ţ�ٵڶ����ɣ���![]() ��
��
�������ݵ�R=0.1m
��2����ţ�ٵڶ����ɵ� ��mgcos�ȩ�mgsin��=ma��
�������ݽ��a=0.4m/s2
��![]() ��s1=1.25m��s����ú�鵽�ﶥ��֮ǰ���봫�ʹ�ȡ�ù�ͬ�ٶȣ�
��s1=1.25m��s����ú�鵽�ﶥ��֮ǰ���봫�ʹ�ȡ�ù�ͬ�ٶȣ�
�ʴ��ʹ����ٶ�Ϊ1m/s��
��3����v=at1���ú������˶���ʱ��t1=2.5s
ú�������˶���λ��Ϊ s2=s��s1=1.75m��
�����ú�������˶���ʱ��t2=1.75s
ú���ڴ��ʹ���ֱ�߲����˶���ʱ�� t=t1+t2
�������ݽ�� t=4.25s
�𣺣�1�������ֵİ뾶Ϊ0.1m��
��2�����ʹ������˶����ٶ�Ϊ1m/s��
��3��ú���ڴ��ʹ���ֱ�߲����˶���ʱ��Ϊ4.25s��