题目内容
13.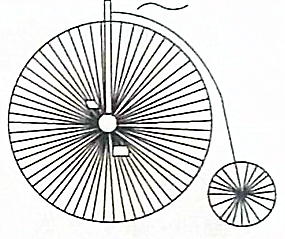 如图所示,早期的自行车是靠前轮驱动的,曲柄组(脚踏)与前轮共轴,前轮半径r1=60cm,后轮半径r2=20cm,若人骑车时的脚踏转速n=45r/min.则前轮的角速度大小为多少?后轮边缘的线速度大小为多少?
如图所示,早期的自行车是靠前轮驱动的,曲柄组(脚踏)与前轮共轴,前轮半径r1=60cm,后轮半径r2=20cm,若人骑车时的脚踏转速n=45r/min.则前轮的角速度大小为多少?后轮边缘的线速度大小为多少?
分析 由图可知,脚踏与前轮属于同轴转动,则角速度相等;前后轮均不打滑,边缘点的线速度相等,根据公式v=Rω计算线速度的大小.
解答 解:脚踏与前轮属于同轴转动,则角速度相等,所以有:
$ω=2π•n=2π×45r/min=2π•\frac{3}{4}r/s=1.5π$rad/s
前后轮均不打滑,边缘点的线速度相等;根据公式v=Rω,
得:v=ωr1=1.5π×0.6=0.9πm/s
答:前轮的角速度大小为1.5πrad/s,后轮边缘的线速度大小为0.9πm/s.
点评 本题关键是明确线速度、角速度、半径的关系公式v=Rω,基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.一物体静止在光滑水平面上,先对物体施加一个水平向右的恒力F1,经过时间t物体运动到距离出发点为s的位置,此时立即撤去F1,同时对物体施加一水平向左的恒力F2,又经过相同的时间t,物体运动到距离出发点$\frac{s}{2}$的位置,在这一过程中力F1和F2的比可能是( )
| A. | 4:5 | B. | 2:5 | C. | 2:7 | D. | 4:21 |
4. 当宇宙飞船到了月球上空先以速度v绕月球作圆周运动,为了使飞船安全的落在月球上的B点,在轨道A点点燃飞船发动器作出短时间的发动给飞船以推力,推力的方向为( )
当宇宙飞船到了月球上空先以速度v绕月球作圆周运动,为了使飞船安全的落在月球上的B点,在轨道A点点燃飞船发动器作出短时间的发动给飞船以推力,推力的方向为( )
 当宇宙飞船到了月球上空先以速度v绕月球作圆周运动,为了使飞船安全的落在月球上的B点,在轨道A点点燃飞船发动器作出短时间的发动给飞船以推力,推力的方向为( )
当宇宙飞船到了月球上空先以速度v绕月球作圆周运动,为了使飞船安全的落在月球上的B点,在轨道A点点燃飞船发动器作出短时间的发动给飞船以推力,推力的方向为( )| A. | 与v的方向一致 | B. | 与v的方向相反 | C. | 垂直v的方向向右 | D. | 垂直v的方向向左 |
1.下列关于加速度的描述,正确的是( )
| A. | 加速度在数值上等于单位时间里速度的变化 | |
| B. | 当加速度与速度方向虽相同但数值减小时,物体做减速运动 | |
| C. | 加速度与速度方向相同 | |
| D. | 物体速度为零时,加速度一定为零 |
5.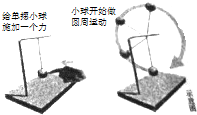 神十航天员王亚平在太空授课时做了图示的实验,用细线悬挂小球,给小球施加一个力后,小球开始在竖直平面内做匀速圆周运动,设神十处于完全失重状态,则小球在运动过程中( )
神十航天员王亚平在太空授课时做了图示的实验,用细线悬挂小球,给小球施加一个力后,小球开始在竖直平面内做匀速圆周运动,设神十处于完全失重状态,则小球在运动过程中( )
 神十航天员王亚平在太空授课时做了图示的实验,用细线悬挂小球,给小球施加一个力后,小球开始在竖直平面内做匀速圆周运动,设神十处于完全失重状态,则小球在运动过程中( )
神十航天员王亚平在太空授课时做了图示的实验,用细线悬挂小球,给小球施加一个力后,小球开始在竖直平面内做匀速圆周运动,设神十处于完全失重状态,则小球在运动过程中( )| A. | 小球所受合力为零 | |
| B. | 重力与细绳的拉力平衡 | |
| C. | 小球只受到细绳的拉力作用 | |
| D. | 细绳的拉力提供了小球作图示运动的向心力 |
2. 如图所示是某型号电吹风的电路图,它主要由电动机M和电热丝R构成.已知电吹风的额定电压为220V,吹冷风时的功率为120W,吹热风时的功率为1000W.关于该电吹风,下列说法正确的是( )
如图所示是某型号电吹风的电路图,它主要由电动机M和电热丝R构成.已知电吹风的额定电压为220V,吹冷风时的功率为120W,吹热风时的功率为1000W.关于该电吹风,下列说法正确的是( )
 如图所示是某型号电吹风的电路图,它主要由电动机M和电热丝R构成.已知电吹风的额定电压为220V,吹冷风时的功率为120W,吹热风时的功率为1000W.关于该电吹风,下列说法正确的是( )
如图所示是某型号电吹风的电路图,它主要由电动机M和电热丝R构成.已知电吹风的额定电压为220V,吹冷风时的功率为120W,吹热风时的功率为1000W.关于该电吹风,下列说法正确的是( )| A. | 若S1、S2闭合,则电吹风吹冷风 | |
| B. | 电热丝的电阻为55Ω | |
| C. | 电动机工作时输出的机械功率为880W | |
| D. | 当电吹风吹热风时,电动机每秒钟消耗的电能为120J |
3.一个运动员参加百米赛跑比赛,经过中点时的速度是11.8m/s,10s到达终点时,速度是11.2m/s,则此运动员百米赛跑的平均速度大小是( )
| A. | 10m/s | B. | 11.2m/s | C. | 11.5m/s | D. | 11.8m/s |
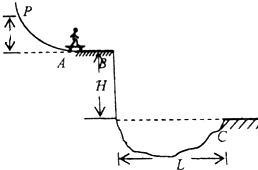 如图所示,滑板运动员从水平台A端相切的圆弧上的P点由静止下滑,滑行至B端后,水平成功飞跃落差H=18m的壕沟,已知P点距水平台AB高h=0.8m,运动员与装备整体可视为质点且设总质量为m,不计摩擦等阻力,g=10m/s2,求:
如图所示,滑板运动员从水平台A端相切的圆弧上的P点由静止下滑,滑行至B端后,水平成功飞跃落差H=18m的壕沟,已知P点距水平台AB高h=0.8m,运动员与装备整体可视为质点且设总质量为m,不计摩擦等阻力,g=10m/s2,求: