题目内容
如图,质量分别为mA和mB的两小球带有同种电荷,电荷量分别为qA和qB,用绝缘细线悬挂在天花板上,平衡时,两小球恰处于同一水平位置,细线与竖直方向间夹角分别为θ1与θ2(θ1>θ2),两小球突然失去各自所带电荷后开始摆动,最大速度分别为vA和vB,最大动能分别为EkA和EkB,则( )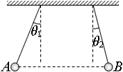
| A.qA一定小于qB | B.mA一定小于mB |
| C.vA一定大于vB | D.EkA一定大于EkB |
BCD
解析试题分析:对小球,均受重力mg和水平库仑力F和细线的拉力T,根据平衡条件可知:F=mgtanθ,根据牛顿第三定律可知FA=FB,又因为θ1>θ2,所以有mA<mB,与电量q无关,故选项A错误;选项B正确;当两球所带电荷突然失去后,库仑力突然消失,两球将分别绕悬点摆动,摆动过程中只有各自的重力做功,以开始时两球的水平连线所在水平面为零势能面,则有EA=EB,根据机械能守恒定律可知,摆到最低点时速度最大,动能亦最大,有:mgl(1-cosθ)= ,解得:v=
,解得:v= ,根据图中几何关系可知:lAcosθ1=lBcosθ2,结合θ1>θ2,可以判断出lA>lB,有vA>vB,故选项C正确;Ek=
,根据图中几何关系可知:lAcosθ1=lBcosθ2,结合θ1>θ2,可以判断出lA>lB,有vA>vB,故选项C正确;Ek= =mgl(1-cosθ)=
=mgl(1-cosθ)= l(1-cosθ)=Flcosθ
l(1-cosθ)=Flcosθ =Flcosθtan
=Flcosθtan ,显然有:FAlAcosθ1=FBlBcosθ2、tan
,显然有:FAlAcosθ1=FBlBcosθ2、tan >tan
>tan ,所以有:EkA>EkB,故选项D正确。
,所以有:EkA>EkB,故选项D正确。
考点:本题主要考查了库仑定律、共点力平衡条件、牛顿第三定律、机械能守恒定律的应用,以及运用数学知识处理物理问题的能力问题,属于中档偏高题。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案如图所示,在特制的弹簧秤下挂一吊篮A,吊篮内挂一重物B,一人站在吊篮中,当此人用100N的竖直向下的力拉重物时,下列说法中正确的是( )
| A.弹簧秤示数不变 |
| B.人对底板的压力减小100N |
| C.B的合力增大100N |
| D.A 的合力不变 |
如图所示,水平地面上有一楔形物块a,倾角为θ=37°,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上。a与b之间光滑,a与b以共同速度在地面轨道的光滑段向左匀速运动。当它们刚运行至轨道的粗糙段时(物块a与粗糙地面的动摩擦因数为μ,g=10m/s2),( )
| A.若μ=0.1,则细绳的张力为零,地面对a的支持力变小 |
| B.若μ=0.1,则细绳的张力变小,地面对a 的支持力不变 |
| C.若μ=0.75,则细绳的张力减小,斜面对b的支持力不变 |
| D.若μ=0.75,则细绳的张力为零,斜面对b的支持力增大 |
用一清绳将小球P系于光滑墙壁上的O点,在墙壁和球P之间夹有一矩形物块Q,如图所示。P、Q均处
于静止状态,则下列说法正确的是( )
| A.Q受到3个力 |
| B.P物体受4个力 |
| C.若绳子变短,Q受到的静摩擦力将增大 |
| D.若绳子变短,绳子的拉力将变小 |
用绝缘细线将一个质量为m、带电量为q的小球悬挂在天花板下面,设空间中存在着沿水平方向的匀强电场.当小球静止时把细线烧断(空气阻力不计).小球将做( )
| A.自由落体运动 |
| B.曲线运动 |
| C.沿悬线的延长线做匀加速直线运动 |
| D.变加速直线运动 |
如图所示,倾角为30°的斜面体固定在水平地面上,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的滑轮O(可视为质点).A的质量为m,B的质量为4m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中B始终保持静止.则在绳子到达竖直位置之前,下列说法正确的是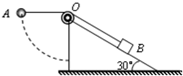
| A.物块B受到的摩擦力一直沿着斜面向上 |
| B.物块B受到的摩擦力先减小后增大 |
| C.绳子的张力一直增大 |
| D.地面对斜面体的摩擦力方向一直水平向右 |
在水平桌面上叠放着木块P和Q,用水平力F推Q,使P、Q两木块一起沿水平桌面匀速滑动,如图所示,以下说法中正确的是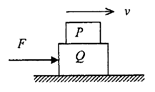
| A.P受3个力,Q受6个力 |
| B.P受4个力,Q受6个力 |
| C.P受2个力,Q受5个力 |
| D.P受2个力,Q受4个力 |
如图所示,两根直木棍AB和CD相互平行,固定在同一个水平面上,一个圆柱形工件P架在两木棍之间,在水平向右的推力F的作用下,恰好能向右匀速运动。若保持两木棍在同一水平面内,但将它们间的距离稍微增大一些后固定.将该圆柱形工件P架在两木棍之间,用同样的水平推力F向右推该工件,则下列说法中正确的是( )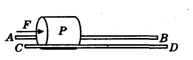
| A.该工件仍可能向右匀速运动 |
| B.该工件P可能向右加速运动 |
| C.AB棍受到的摩擦力一定大于F/2 |
| D.AB棍受到的摩擦力一定等于F/2 |