题目内容
【题目】蹦床比赛分成预备运动和比赛动作。最初，运动员静止站在蹦床上在预备运动阶段，他经过若干次蹦跳，逐渐增加上升高度，最终达到完成比赛动作所需的高度；此后，进入比赛动作阶段。
把蹦床简化为一个竖直放置的轻弹簧，弹力大小F="kx" (x为床面下沉的距离，k为常量)。质量m=50kg的运动员静止站在蹦床上，床面下沉x0=0.10m；在预备运动中，假设运动员所做的总共W全部用于其机械能；在比赛动作中，把该运动员视作质点，其每次离开床面做竖直上抛运动的腾空时间均为△t=2.0s，设运动员每次落下使床面压缩的最大深度均为xl。取重力加速度g=10m/s2，忽略空气阻力的影响。
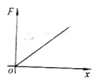
（1）求常量k，并在图中画出弹力F随x变化的示意图；
（2）求在比赛动作中，运动员离开床面后上升的最大高度hm；
（3）借助F-x 图像可以确定弹性做功的规律，在此基础上，求x1和W的值
【答案】（1）k=5000N/m （2）5m （3）W=2525J
【解析】
试题（1）床面下沉x0=0.1m时，运动员受力平衡，有mg=kx0，解得k=5×103N/m。
F-x图线如图所示。
（2）运动员从x=0处离开床面，开始腾空，由运动的对称性知其上升、下落的时间相等，
，解得hm=5.0m。
（3）参照由速度时间图线求位移的方法可知F-x图线下的面积等于弹力做的功，从x处到x=0处，弹力做的功
，
运动员从x1处上升到最大高度hm的过程，根据动能定理可得
，解得x1=1.1m
对整个预备运动过程分析，由题设条件以及功和能的关系，有
解得W=2525J.
练习册系列答案
相关题目
