题目内容
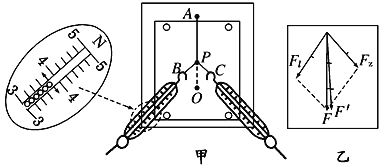
【题目】所受重力G1=8N的砝码悬挂在绳PA和PB的结点上.PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求: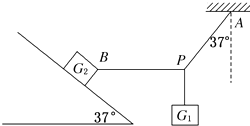
(1)木块与斜面间的摩擦力;
(2)木块所受斜面的弹力.
【答案】
(1)解:如图甲所示分析结点P受力,由平衡条件得:
FAcos37°=G1
FAsin37°=FB
可解得:BP绳的拉力为FB=6 N
再分析G2的受力情况如图乙所示.
由物体的平衡条件可得:
Ff=G2sin37°+FB′cos37°
FN+FB′sin37°=G2 cos37°
又有FB′=FB
解得:Ff=64.8N,FN=76.4N
答:木块与斜面间的摩擦力大小为64.8 N.

(2)解:如图甲所示分析结点P受力,由平衡条件得:
FAcos37°=G1
FAsin37°=FB
可解得:BP绳的拉力为FB=6 N
再分析G2的受力情况如图乙所示.
由物体的平衡条件可得:
Ff=G2sin37°+FB′cos37°
FN+FB′sin37°=G2 cos37°
又有FB′=FB
解得:Ff=64.8N,FN=76.4N
答:木块所受斜面的弹力大小为76.4 N,方向垂直斜面向上

【解析】先以结点P为研究对象,分析受力情况,由平衡条件求出BP绳的拉力大小,再以G2为研究对象,分析受力,作出力图,根据平衡条件求解斜面对木块的摩擦力和弹力.
【考点精析】通过灵活运用静摩擦力,掌握静摩擦力:静摩擦力大小可在0与fmax 之间变化,一般应根据物体的运动状态由平衡条件或牛顿定律来求解即可以解答此题.

练习册系列答案
相关题目