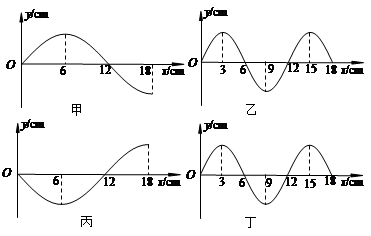Question

一根张紧的水平弹性绳上的a，b两点，相距14.0m，b点在a点的右方．如图所示．当一列简谐横波沿此长绳向右传播时，若a点的位移达到正向最大时，b点的位移恰为零，且向下运动，经过1.0s后，a点的位移为零且向下运动，而b点的位移恰达到负最大，则这列简谐横渡的波速可能等于

A．2m/s B．4.67m/s C．6m/s D．10m/s

 

Answer 1

ABD

本题是通过描述一列波中两个质点振动情况及其关系来了解整列波特性的题，其方法是先在波形图上找到a点与其对应的可能的b点，再把题中a，b两点的距离与波长联系起来，时间与周期联系起来，找到λ，再用公式v＝λ/T求得波速．
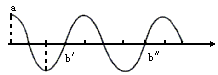
　　依题可画出波形图，a点位移达正向最大，b点可能位置用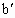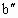，代表，正经平衡位置向下．可见a，b间距与波长关系为：
　　＝(n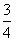＋)λ，(n＝0，1，2，…)
　　∴λ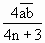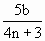＝＝m．
　　时间Δt＝1.0s与周期关系为：
　　Δt＝(k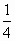＋)T，(k＝0，1，2，…)
　　∴T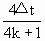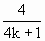＝＝s．
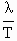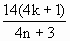　　∴波速v＝＝m/s．
　　当n＝0，k＝0时，v＝4.67m/s，故B选项正确；
　　当n＝1，k＝0时，v＝2m/s，故A选项正确；
　　当n＝1，k＝1时，v＝10m/s，故D选项正确；
★ 试题错析： 思维诊断：部分学生建立不起距离与波长、时间与周期的联系，写不出速度表达式来．处理这类问题时，画出波形图，找出以上关系是关键．部分学生没有注意到周期，漏选A，D项，或者没有用好自然数k与n，或者认为k＝n而漏选A项．