题目内容
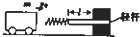
某缓冲装置的理想模型如图所示，劲度系数足够大的轻质弹簧与轻杆相连，轻杆可在固定的槽内移动，与槽间的滑动摩擦力恒为Ff。轻杆向右移动不超过l时，装置可安全工作。一质量为m的小车若以速度v0撞击弹簧，将导致轻杆向右移动
。轻杆与槽间的最大静摩擦力等于滑动摩擦力，且不计小车与地面的摩擦。
(1)若弹簧的劲度系数为k，求轻杆开始移动时，弹簧的压缩量x；
(2)求为使装置安全工作，允许该小车撞击的最大速度vm。
【解题指南】解答本题时可按以下思路分析：
(1)根据胡克定律求解弹簧的压缩量；
(2)小车每次撞击时克服弹簧的弹力做功相同；
(3)撞击时小车克服弹力和摩擦力做功。
【解析】(1)轻杆开始移动时，弹簧的弹力
F=kx (2分)
且F=Ff (2分)
解得x=
(2分)
(2)设轻杆移动前小车对弹簧所做的功为W，则小车从撞击到停止的过程中
由动能定理得
(2分)
同理，小车以vm撞击弹簧时
(2分)
解得
(2分)
答案：(1) (2)
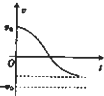
某缓冲装置的理想模型如图所示，劲度系数足够大的轻质弹簧与轻杆相连，轻杆可在固定的槽内移动，与槽间的滑动摩擦力为定值．轻杆向右移动不超过l时，装置可安全工作．若一小车以速度v0撞击弹簧，已知装置可安全工作，轻杆与槽间的最大静摩擦力等于滑动摩擦力，且不计小车与地面间的摩擦．从小车与弹簧刚接触时开始计时，下列关于小车运动的速度-时间图象可能正确的是（ ）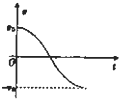
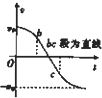
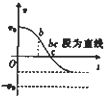
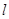时，装置可安全工作。 一质量为m 的小车若以速度
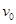撞击弹簧，可使轻杆向右移动了
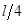。轻杆与槽间的最大静摩擦力等于滑动摩擦力，且不计小车与地面的摩擦。
