题目内容
6. 摆长为l的单摆做小角度摆动,若摆球的质量为m,最大偏角为α(α<5°),则:
摆长为l的单摆做小角度摆动,若摆球的质量为m,最大偏角为α(α<5°),则:(1)摆球经过最低点时的速度是多大?
(2)摆球经过最低点时,摆线拉力多大?
(3)摆球经过A点时,摆线拉力多大?
(4)摆球所受回复力的最大值多少?
分析 (1)根据机械能守恒定律,即可求解;
(2、3)根据牛顿第二定律,即可求解;
(4)根据回复力定义,结合受力分析,即可求解.
解答 解:(1)根据机械能守恒定律,则有:$\frac{1}{2}m{v}^{2}=mgl(1-cosθ)$;
解得:v=$\sqrt{2gl(1-cosθ)}$;
(2)根据牛顿第二定律,则有:T-mg=m$\frac{{v}^{2}}{l}$
解得:T=mg(2-cosθ)
(3)摆球经过A点时,速度等于零,则摆线拉力T′=mgcosα
(4)根据回复力的定义,则有摆球所受回复力的最大值mgsinα
答:(1)摆球经过最低点时的速度是$\sqrt{2gl(1-cosθ)}$;
(2)摆球经过最低点时,摆线拉力mg(2-cosθ);
(3)摆球经过A点时,摆线拉力=mgcosα;
(4)摆球所受回复力的最大值mgsinα.
点评 考查机械能守恒定律的应用,掌握牛顿第二定律的内容,注意回复力的定义,同时理解力的矢量合成法则.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
16.一个带电体能被看作点电荷的条件是( )
| A. | 带电体的线度足够小 | |
| B. | 带电体的长度与它到场点的距离相比足够小 | |
| C. | 带电体所带的电量足够小 | |
| D. | 带电体的线度及带电量都足够小 |
14.一质点沿直线运动时的速度-时间图象如图所示,则以下说法正确的是( )


| A. | 第1s内和第2s内的速度方向相反 | B. | 第2s内的速度和加速度方向相反 | ||
| C. | 前 4s内质点的位移为零 | D. | 第3s末和第5s末质点的位置相同 |
1.将水平弹簧振子从其平衡位置O拉开到位置A然后自由释放.若OA距离增大,则下列判断中正确的是( )
| A. | 振动的位移要大些 | B. | 振动的周期要长些 | ||
| C. | 振动的频率要大些 | D. | 振动的能量要大些 |
11.下列物体中能看作质点的是( )
| A. | 研究沿着斜面下滑的木块的运动情况 | |
| B. | 从北京驶往广州的火车的载客量 | |
| C. | 研究地球自转情况的地球 | |
| D. | 对旋转着的电扇的扇叶受力方面的分析 |
10.关于曲线运动,下列说法中正确的是( )
| A. | 某点的速度方向为该点切线方向 | B. | 曲线运动一定是变速运动 | ||
| C. | 物体的速度方向时刻改变 | D. | 曲线运动可能是匀速运动 |
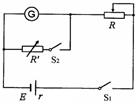 将满偏电流Ig=300μA、内阻未知的电流表G改装成电压表并进行核对.
将满偏电流Ig=300μA、内阻未知的电流表G改装成电压表并进行核对.