题目内容
1. 如图1,质量m=1kg的物体,初速度为v0,方向水平向右.在向右的水平拉力F的作用下,沿粗糙水平面运动,位移为4m时,拉力F停止作用,物体又运动了4m后停下来.其运动过程中的动能位移的变化(Ek-x)图线如图2所示,重力加速度g取10m/s2,则下列判断正确的是( )
如图1,质量m=1kg的物体,初速度为v0,方向水平向右.在向右的水平拉力F的作用下,沿粗糙水平面运动,位移为4m时,拉力F停止作用,物体又运动了4m后停下来.其运动过程中的动能位移的变化(Ek-x)图线如图2所示,重力加速度g取10m/s2,则下列判断正确的是( )| A. | 物体的初速度v0为 $\sqrt{2}$m/s | |
| B. | 拉力F的大小为2N | |
| C. | 物体与水平面间的动摩擦因数为0.25 | |
| D. | 全程物体克服合力做功为2J |
分析 本题应抓住:动能与速度的关系:Ek=$\frac{1}{2}m{v}^{2}$,即可求出初速度;对撤去拉力F后直到停止的过程运用动能定理,求解动摩擦因数;滑动摩擦力的大小f=μmg;对加速运动过程,根据动能定理可求得F的大小.
解答 解:A、由图可知物体的初动能为2J,根据Ek=$\frac{1}{2}m{v}^{2}$,得:v0=2m/s.故A错误.
BC、设匀加速的位移为s1,匀减速运动的位移为s2,由图知:s1=4m,s2=4m
对撤去拉力F后直到停止的过程运用动能定理得:-μmgs2=0-10J,得μ=0.25
对于匀加速运动过程,由动能定理得:Fs1-fs1=10J-2J
解得,F=4.5N 故B错误,C正确.
D、滑动摩擦力的大小f=μmg=2.5N,所以Wf=-fs=-2.5×8J=-2J,故D 正确.
故选:CD.
点评 本题是个图象问题,要从图象中获取正确有用的信息来解题,熟练运用动能定理和做功公式即可解题,常规题.

练习册系列答案
相关题目
11.质量相同的两个小球在光滑水平面上沿连心线同向运动,球1的动量为7kg•m/s,球2的动量为5kg•m/s,当球1追上球2时发生碰撞,则碰撞后两球动量变化的可能值是( )
| A. | △p1=-1 kg•m/s,△p2=1 kg•m/s | B. | △p1=-1 kg•m/s,△p2=4 kg•m/s | ||
| C. | △p1=-9 kg•m/s,△p2=9 kg•m/s | D. | △p1=-12 kg•m/s,△p2=10 kg•m/s |
9.宇航员在围绕地球做匀速圆周运动的航天飞机中,处于完全失重状态,则下列说法中正确的是( )
| A. | 宇航员不受重力作用 | |
| B. | 宇航员只受重力作用且由重力产生向心加速度 | |
| C. | 宇航员不只受到重力的作用 | |
| D. | 宇航员受到平衡力的作用 |
16. 在做“探究功与物体速度变化的关系”的实验时,小车的质量为m,使用橡皮筋6根,每次增加一根,实验中W、v、v2的数据已填在下面表格中.
在做“探究功与物体速度变化的关系”的实验时,小车的质量为m,使用橡皮筋6根,每次增加一根,实验中W、v、v2的数据已填在下面表格中.
(1)在图甲乙两坐标系中选择合适的坐标系作出图象.
(2)从图象可以得出的实验结论是从乙图看出W∝v2.
 在做“探究功与物体速度变化的关系”的实验时,小车的质量为m,使用橡皮筋6根,每次增加一根,实验中W、v、v2的数据已填在下面表格中.
在做“探究功与物体速度变化的关系”的实验时,小车的质量为m,使用橡皮筋6根,每次增加一根,实验中W、v、v2的数据已填在下面表格中.| W | v/m•s-1 | v2/m2•s-2 |
| 0 | 0 | 0 |
| 1.00 | 0.80 | 0.64 |
| 2.00 | 1.10 | 1.21 |
| 3.00 | 1.28 | 1.64 |
| 4.00 | 1.53 | 2.34 |
| 5.00 | 1.76 | 3.10 |
| 6.00 | 1.89 | 3.57 |
(2)从图象可以得出的实验结论是从乙图看出W∝v2.
13.一列简谐横波,在t=0.6s时刻的图象如图甲所示,波上A质点的振动图象如图乙所示,则以下说法正确的是( )


| A. | 这列波沿x轴正方向传播,波速是$\frac{50}{3}$m/s | |
| B. | 从t=0.6s开始,紧接着的△t=0.6s时间内,A质点通过的路程是4m | |
| C. | 从t=0.6s开始,质点P比质点Q早0.4s到达波峰位置 | |
| D. | 从t=0.6s开始,再经0.15s质点Q第一次到达波谷位置 |
10.假设地球同步卫星的轨道半径是地球半径的n倍,则( )
| A. | 同步卫星运行速度是第一宇宙速度的$\frac{1}{n}$倍 | |
| B. | 同步卫星的运行速度是第一宇宙速的$\sqrt{\frac{1}{n}}$倍 | |
| C. | 同步卫星的运行速度是地球赤道上物体随地球自转速度的$\frac{1}{n}$倍 | |
| D. | 同步卫星的向心加速度是地球表面重力加速度的$\frac{1}{n}$倍 |
11. 光滑绝缘曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程是y=x2,下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属球从抛物线上y=b(b>a)处沿抛物线自由下滑,忽略空气阻力,重力加速度值为g.则( )
光滑绝缘曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程是y=x2,下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属球从抛物线上y=b(b>a)处沿抛物线自由下滑,忽略空气阻力,重力加速度值为g.则( )
 光滑绝缘曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程是y=x2,下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属球从抛物线上y=b(b>a)处沿抛物线自由下滑,忽略空气阻力,重力加速度值为g.则( )
光滑绝缘曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程是y=x2,下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属球从抛物线上y=b(b>a)处沿抛物线自由下滑,忽略空气阻力,重力加速度值为g.则( )| A. | 小金属球沿抛物线下滑后最终停在O点 | |
| B. | 小金属球沿抛物线下滑后每次过O点速度一直在减小 | |
| C. | 小金属球沿抛物线下滑后对O点压力一定大于mg | |
| D. | 小金属球沿抛物线下滑后最终产生的焦耳热总量是mg(b-a) |
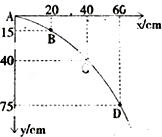 某同学在做研究平抛运动的试验时,忘记记下斜槽位置,如图所示中的A点为小球运动一段时间后的位置,他便以A为坐标原点,建立了水平方向和竖直方向的坐标轴,得到如图所示的图象,试根据图象求出:(g取10m/s2)
某同学在做研究平抛运动的试验时,忘记记下斜槽位置,如图所示中的A点为小球运动一段时间后的位置,他便以A为坐标原点,建立了水平方向和竖直方向的坐标轴,得到如图所示的图象,试根据图象求出:(g取10m/s2)


