题目内容
15. 在竖直平面内有一个光滑的半圆轨道,轨道两端连线即直径在竖直方向,轨道半径为0.9m,一个质量为0.5kg的小球以一定的初速度滚上轨道(g取10m/s2,结果保留一位小数)求:
在竖直平面内有一个光滑的半圆轨道,轨道两端连线即直径在竖直方向,轨道半径为0.9m,一个质量为0.5kg的小球以一定的初速度滚上轨道(g取10m/s2,结果保留一位小数)求:(1)小球在最高点不脱离轨道的最小速率是多少?
(2)小球在最高点速率v=4m/s时,小球对轨道的压力是多少?
(3)小球以v=8m/s的速率从最高点离开轨道,落地时的速度大小是多少?方向如何?
分析 (1)在最高点小球不脱离轨道的条件是重力不大于小球做圆周运动所需要的向心力,由牛顿第二定律列式求解最小速度.
(2)由牛顿第二定律列式求解轨道对小球的压力,进而求解小球对轨道的压力
(3)从最高点离开轨道,做平抛运动,由运动分解与合成的知识求解.
解答 解:(1)在最高点小球不脱离轨道的条件是重力不大于小球做圆周运动所需要的向心力
即mg≤m$\frac{{v}^{2}}{r}$
则所求的最小速率vmin=$\sqrt{gr}$=$\sqrt{10×0.9}$=3m/s
(2)因为v=4m/s>vmin,所以轨道对小球有一定的压力F
则 F+mg=m$\frac{{v}^{2}}{r}$
所以 F=m$\frac{{v}^{2}}{r}$-mg=0.5×$\frac{{4}^{2}}{0.9}$-5≈3.9N
由牛顿第三定律知,小球对轨道的压力F′=F=3.9N
(3)小球以v=8m/s的速率从最高点离开轨道后做平抛运动,则
2r=$\frac{1}{2}$gt2
所以t=2$\sqrt{\frac{r}{g}}$=2×$\sqrt{\frac{0.9}{10}}$=0.6s
落地时竖直方向分速度 vy=gt=6m/s
合速度 v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10m/s
设落地速度与水平方向的夹角为θ
则tanθ=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{6}{8}$=0.75,则θ=37°
答:
(1)小球在最高点不脱离轨道的最小速率是3m/s
(2)小球对轨道的压力是3.9N
(3)落地时的速度大小是10m/s,方向与水平方向的夹角为37°.
点评 本题主要考查了向心力公式及平抛运动基本公式的直接应用.要掌握竖直平面内圆周运动临界条件:重力充当向心力,得到最小速度为$\sqrt{gr}$.

 名校课堂系列答案
名校课堂系列答案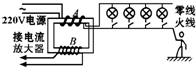 如图所示是一种触电保安器,变压器的A部分用火线和零线双股平行绕制而成,其左右分别与220V交流电源和用电器相连;B部分有一个单股线圈,接到电流放大器上,一旦B线圈中有电流,经过放大器能够带动继电器切断电源.关于以上说法正确的是( )
如图所示是一种触电保安器,变压器的A部分用火线和零线双股平行绕制而成,其左右分别与220V交流电源和用电器相连;B部分有一个单股线圈,接到电流放大器上,一旦B线圈中有电流,经过放大器能够带动继电器切断电源.关于以上说法正确的是( )| A. | 多开灯或者启动其他用电器,不会使保安器切断电源 | |
| B. | 图示中,某人用手只接触火线引起单线触电时,保安器会切断电源 | |
| C. | 如果某人用手同时接触火线和零线引起双线触电时,保安器会切断电源 | |
| D. | 当用电器电路中负载超荷时,保安器会立即切断电源 |
| A. | 当振子从O向A′运动时,位移变小 | B. | 当振子从A′向O运动时,速度变小 | ||
| C. | 当振子从O向A运动时,加速度变小 | D. | 当振子从A向O运动时,回复力变小 |
| A. | 合运动的速度一定大于分运动的速度 | |
| B. | 合运动的速度一定小于分运动的速度 | |
| C. | 合运动的时间一定大于分运动的时间 | |
| D. | 合运动就是物体的实际运动 |
| A. | 两个力的合力大小一定大于其中一个分力大小 | |
| B. | 两个力的合力的大小一定大于两个分力大小 | |
| C. | 两个力的合力的大小可以小于其中一个分力的大小,但不能比两个分力都小 | |
| D. | 两个力的合力的大小可以比两个分力都大,也可以比两个分力都小 |
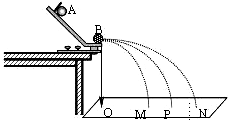 验证动量守恒实验装置的如图所示:
验证动量守恒实验装置的如图所示: