题目内容
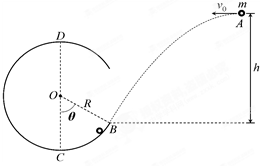 如图一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与竖直方向夹角θ=60°,C为轨道最低点,D为轨道最高点.一个质量m=0.50kg的小球(视为质点)从空中A点以v0=4.0m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.重力加速度g=10m/s2.求:
如图一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与竖直方向夹角θ=60°,C为轨道最低点,D为轨道最高点.一个质量m=0.50kg的小球(视为质点)从空中A点以v0=4.0m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.重力加速度g=10m/s2.求:(1)小球抛出点A距圆弧轨道B端的高度h;
(2)小球能否到达轨道最高点D?若能到达,求小球对D点的压力;若不能到达,说明理由.
分析:(1)根据小球恰好从轨道的B端沿切线方向进入轨道,说明小球的末速度应该沿着B点切线方向,再由圆的半径和角度的关系,可以求出B点切线的方向,即平抛末速度的方向,从而可以求得竖直方向分速度,进而求出高度;
(2)设小球能到达D点,根据机械能守恒定律求得D点速度,再运用牛顿第二定律和圆周运动知识求解.
(2)设小球能到达D点,根据机械能守恒定律求得D点速度,再运用牛顿第二定律和圆周运动知识求解.
解答:解:(1)小球恰好从轨道的B端沿切线方向进入轨道,说明小球的末速度应该沿着B点切线方向,
将平抛末速度进行分解,根据几何关系得:
B点速度在竖直方向的分量:vy=v0tan60°=4
m/s
竖直方向的分运动为自由落体运动.h=
=
=2.4m
(2)设小球能到达D点,根据机械能守恒定律,有
mvD2=
mv02+mg(h-R-Rcosθ)
解得vD=
m/s>
=
m/s,即小球能到达D点.
根据牛顿定律,有F′D+mg=m
代入数据,解得小球受到的压力F′D=12N
根据牛顿第三定律,小球对轨道的压力为FD=F′D=12N,方向竖直向上.
答:(1)小球抛出点A距圆弧轨道B端的高度h是2.4m.
(2)小球能到达D点,对D点的压力是12N,方向竖直向上.
将平抛末速度进行分解,根据几何关系得:
B点速度在竖直方向的分量:vy=v0tan60°=4
| 3 |
竖直方向的分运动为自由落体运动.h=
| vy2 |
| 2g |
| 48 |
| 20 |
(2)设小球能到达D点,根据机械能守恒定律,有
| 1 |
| 2 |
| 1 |
| 2 |
解得vD=
| 34 |
| gR |
| 10 |
根据牛顿定律,有F′D+mg=m
| vD2 |
| R |
代入数据,解得小球受到的压力F′D=12N
根据牛顿第三定律,小球对轨道的压力为FD=F′D=12N,方向竖直向上.
答:(1)小球抛出点A距圆弧轨道B端的高度h是2.4m.
(2)小球能到达D点,对D点的压力是12N,方向竖直向上.
点评:恰能无碰撞地沿圆弧切线从B点进入光滑竖直圆弧轨道,这是解这道题的关键,理解了这句话就可以求得小球的末速度,本题很好的把平抛运动和圆周运动结合在一起运用机械能守恒解决,能够很好的考查学生的能力,是道好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012?东至县二模)如图,半径R=1.0m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=0.5m的水平面BC相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=37°的光滑斜面连接,质量m=1.0kg的小滑块从圆弧上某点由静止释放,到达圆弧B点时小滑块对圆弧的压力刚好等于其重力的2倍,当小滑块运动到C点时与一个质量M=2.0kg的小球正碰,碰后返回恰好停在B点,已知滑块与水平面间的动摩擦因数?=0.1.(sin37°=0.6 cos37°=0.8,g取l0m/s2)
(2012?东至县二模)如图,半径R=1.0m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=0.5m的水平面BC相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=37°的光滑斜面连接,质量m=1.0kg的小滑块从圆弧上某点由静止释放,到达圆弧B点时小滑块对圆弧的压力刚好等于其重力的2倍,当小滑块运动到C点时与一个质量M=2.0kg的小球正碰,碰后返回恰好停在B点,已知滑块与水平面间的动摩擦因数?=0.1.(sin37°=0.6 cos37°=0.8,g取l0m/s2) 如图,半径R=1.0m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=0.5m的水平面BC相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=37°的光滑斜面连接,质量m=1.0kg的小滑块从圆弧上某点由静止释放,到达圆弧B点时小滑块对圆弧的压力刚好等于其重力的2倍,当小滑块运动到C点时与一个质量M=2.0kg的小球正碰,碰后返回恰好停在B点,已知滑块与水平面间的动摩擦因数µ=0.1.(sin37°=0.6 cos37°=0.8,g取l0m/s2)
如图,半径R=1.0m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=0.5m的水平面BC相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=37°的光滑斜面连接,质量m=1.0kg的小滑块从圆弧上某点由静止释放,到达圆弧B点时小滑块对圆弧的压力刚好等于其重力的2倍,当小滑块运动到C点时与一个质量M=2.0kg的小球正碰,碰后返回恰好停在B点,已知滑块与水平面间的动摩擦因数µ=0.1.(sin37°=0.6 cos37°=0.8,g取l0m/s2)
 如图,半径R=1.0m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=0.5m的水平面BC相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=37°的光滑斜面连接,质量m=1.0kg的小滑块从圆弧上某点由静止释放,到达圆弧B点时小滑块对圆弧的压力刚好等于其重力的2倍,当小滑块运动到C点时与一个质量M=2.0kg的小球正碰,碰后返回恰好停在B点,已知滑块与水平面间的动摩擦因数µ=0.1.(sin37°=0.6 cos37°=0.8,g取l0m/s2)
如图,半径R=1.0m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=0.5m的水平面BC相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=37°的光滑斜面连接,质量m=1.0kg的小滑块从圆弧上某点由静止释放,到达圆弧B点时小滑块对圆弧的压力刚好等于其重力的2倍,当小滑块运动到C点时与一个质量M=2.0kg的小球正碰,碰后返回恰好停在B点,已知滑块与水平面间的动摩擦因数µ=0.1.(sin37°=0.6 cos37°=0.8,g取l0m/s2)