题目内容
7.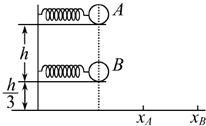 在一个竖直的支架上固定着两个水平的弹簧枪A和B,弹簧枪A、B在同一竖直平面内,如图所示,A比B高h,弹簧枪B的出口距水平面高$\frac{h}{3}$,弹簧枪A、B射出的子弹的水平射程之比为xA:xB=1:2.设弹簧枪A、B的高度差h不变,且射出子弹的初速度不变,要使两个弹簧枪射出的子弹落到水平面上的同一点,则( )
在一个竖直的支架上固定着两个水平的弹簧枪A和B,弹簧枪A、B在同一竖直平面内,如图所示,A比B高h,弹簧枪B的出口距水平面高$\frac{h}{3}$,弹簧枪A、B射出的子弹的水平射程之比为xA:xB=1:2.设弹簧枪A、B的高度差h不变,且射出子弹的初速度不变,要使两个弹簧枪射出的子弹落到水平面上的同一点,则( )| A. | 竖直支架向上移动,移动的距离为$\frac{2h}{15}$ | |
| B. | 竖直支架向下移动,移动的距离为$\frac{2h}{15}$ | |
| C. | 竖直支架向上移动,移动的距离为$\frac{4h}{15}$ | |
| D. | 竖直支架向下移动,移动的距离为$\frac{4h}{15}$ |
分析 平抛运动在竖直方向上做自由落体运动,在水平方向上做匀速直线运动,根据A、B的高度比求出运动的时间比,从而根据水平射程比得出初速度之比,再通过子弹的水平位移相等,求出时间比,从而求出高度比,从而得出竖直支架移动的距离.
解答 解:开始hA=$\frac{4}{3}$h,hB=$\frac{1}{3}$h,根据h=$\frac{1}{2}$gt2得,t=$\sqrt{\frac{2H}{g}}$,则$\frac{{t}_{A}}{{t}_{B}}=2$.
因为$\frac{{x}_{A}}{{x}_{B}}$=$\frac{1}{2}$,根据x=vt,则$\frac{{v}_{A}}{{v}_{B}}$=$\frac{1}{4}$.
调整高度后,水平位移相等,根据x=vt,则运动时间比变为$\frac{{t}_{A}}{{t}_{B}}$=$\frac{4}{1}$.
则竖直位移之比$\frac{{h}_{A}′}{{h}_{B}′}$=$\frac{{t}_{A}^{2}}{{t}_{B}^{2}}=\frac{{4}^{2}}{{1}^{2}}$=$\frac{16}{1}$.
设A的高度为H,有$\frac{H}{H-h}$=$\frac{16}{1}$,解得H=$\frac{16}{15}$h.
则支架下降的距离△h=$\frac{4}{3}$h-$\frac{16}{15}$h=$\frac{4}{15}$h.
故ABCD错误,D正确;
故选:D.
点评 解决本题的关键知道平抛运动的时间由高度决定,时间和初速度共同决定水平位移.

练习册系列答案
相关题目
17.下列关于简谐运动的振幅、周期和频率的说法正确的是( )
| A. | 振幅是矢量,方向从平衡位置指向最大位移处 | |
| B. | 周期和频率的乘积不一定等于1 | |
| C. | 振幅增加,周期必然增加,而频率减小 | |
| D. | 做简谐运动的物体,其频率固定,与振幅无关 |
18.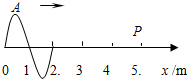 一列简谐横波沿x轴正方向传播,t=0时波形如图所示.已知在0.6s末,A点恰第四次(图中为第一次)出现在波峰,则下列说法正确的是( )
一列简谐横波沿x轴正方向传播,t=0时波形如图所示.已知在0.6s末,A点恰第四次(图中为第一次)出现在波峰,则下列说法正确的是( )
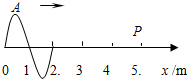 一列简谐横波沿x轴正方向传播,t=0时波形如图所示.已知在0.6s末,A点恰第四次(图中为第一次)出现在波峰,则下列说法正确的是( )
一列简谐横波沿x轴正方向传播,t=0时波形如图所示.已知在0.6s末,A点恰第四次(图中为第一次)出现在波峰,则下列说法正确的是( )| A. | 波的周期是0.6s | |
| B. | 波传播到P点需要1.5s | |
| C. | P点开始振动时速度方向是向上的 | |
| D. | P点在0.35s末第一次出现在波谷底部 |
15.关于地球同步通讯卫星,下列说法中正确的是( )
| A. | 各国发射的这种卫星轨道半径都一样 | |
| B. | 它运行的线速度一定小于第一宇宙速度 | |
| C. | 它一定在赤道上空运行 | |
| D. | 它运行的线速度介于第一和第二宇宙速度之间 |
2.关于布朗运动,如下说法中正确的是( )
| A. | 布朗运动是在显微镜中看到的液体分子的无规则运动 | |
| B. | 布朗运动是液体分子无规则运动的反映 | |
| C. | 悬浮微粒越大,布朗运动越显著 | |
| D. | 液体温度越高,布朗运动越显著 |
12. 如图所示为氢原子的能级图,在具有下列能量的光子或者电子中,不能让基态氢原子吸收能量而发生跃迁的是( )
如图所示为氢原子的能级图,在具有下列能量的光子或者电子中,不能让基态氢原子吸收能量而发生跃迁的是( )
 如图所示为氢原子的能级图,在具有下列能量的光子或者电子中,不能让基态氢原子吸收能量而发生跃迁的是( )
如图所示为氢原子的能级图,在具有下列能量的光子或者电子中,不能让基态氢原子吸收能量而发生跃迁的是( )| A. | 13eV的光子 | B. | 13eV的电子 | C. | 10.2 eV的光子 | D. | 10.2 eV的电子 |
19.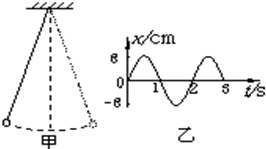 如图甲所示,一个单摆做小角度摆动,从某次摆球由左向右通过平衡位置时开始计时,相对平衡位置的位移x随时间t变化的图象如图乙所示.不计空气阻力,g取10m/s2.对于这个单摆的振动过程,下列说法中正确的是( )
如图甲所示,一个单摆做小角度摆动,从某次摆球由左向右通过平衡位置时开始计时,相对平衡位置的位移x随时间t变化的图象如图乙所示.不计空气阻力,g取10m/s2.对于这个单摆的振动过程,下列说法中正确的是( )
 如图甲所示,一个单摆做小角度摆动,从某次摆球由左向右通过平衡位置时开始计时,相对平衡位置的位移x随时间t变化的图象如图乙所示.不计空气阻力,g取10m/s2.对于这个单摆的振动过程,下列说法中正确的是( )
如图甲所示,一个单摆做小角度摆动,从某次摆球由左向右通过平衡位置时开始计时,相对平衡位置的位移x随时间t变化的图象如图乙所示.不计空气阻力,g取10m/s2.对于这个单摆的振动过程,下列说法中正确的是( )| A. | 单摆的位移x随时间t变化的关系式为x=8sin(πt)cm | |
| B. | 单摆的摆长约为1.0m | |
| C. | 从t=2.5s到t=3.0s的过程中,摆球的重力势能逐渐增大 | |
| D. | 从t=2.5s到t=3.0s的过程中,摆球所受绳子拉力逐渐减小 |
7.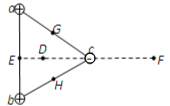 在光滑的绝缘水平面上,有一个正三角形abc,顶点a、b处分别固定一个正点电荷,c处固定一个负点电荷,它们的电荷量大小都相等,如图所示,D点为正三角形外界圆的圆心,E、G、H分别为ab、ac、bc的中点,E、F两点关于c点对称,下列说法中正确的是( )
在光滑的绝缘水平面上,有一个正三角形abc,顶点a、b处分别固定一个正点电荷,c处固定一个负点电荷,它们的电荷量大小都相等,如图所示,D点为正三角形外界圆的圆心,E、G、H分别为ab、ac、bc的中点,E、F两点关于c点对称,下列说法中正确的是( )
 在光滑的绝缘水平面上,有一个正三角形abc,顶点a、b处分别固定一个正点电荷,c处固定一个负点电荷,它们的电荷量大小都相等,如图所示,D点为正三角形外界圆的圆心,E、G、H分别为ab、ac、bc的中点,E、F两点关于c点对称,下列说法中正确的是( )
在光滑的绝缘水平面上,有一个正三角形abc,顶点a、b处分别固定一个正点电荷,c处固定一个负点电荷,它们的电荷量大小都相等,如图所示,D点为正三角形外界圆的圆心,E、G、H分别为ab、ac、bc的中点,E、F两点关于c点对称,下列说法中正确的是( )| A. | D点的场强为零,电势也为零 | |
| B. | G、H两点的场强相同 | |
| C. | E、F两点的电场强度大小相等、方向相反 | |
| D. | 将一带正电的试探电荷有E点移动到D点的过程中,该电荷的电势能减小 |