题目内容
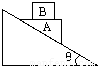
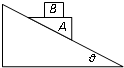 如图,在光滑的倾角为θ的固定斜面上放一个劈形的物体A,质量为M,其上表面水平且粗糙.质量为m的物体B放在A的上面,AB能保持相对静止并一起沿斜面下滑,求
如图,在光滑的倾角为θ的固定斜面上放一个劈形的物体A,质量为M,其上表面水平且粗糙.质量为m的物体B放在A的上面,AB能保持相对静止并一起沿斜面下滑,求(1)A对斜面的压力大小
(2)A对B的支持力大小.
分析:对整体分析,根据牛顿第二定律求出整体的加速度,隔离对B分析,根据正交分解,在竖直方向上根据牛顿第二定律求出A对B的支持力大小.
解答:解:(1)对整体分析,在垂直斜面方向上有:
N=(m+M)gcosθ
则A对斜面的压力为:F=N=(m+M)gcosθ.
在斜面方向上有:(M+m)gsinθ=(M+m)a
解得:a=gsinθ.
(2)将加速度a分解为水平方向和竖直方向,有:
ay=gsinθ?sinθ=gsin2θ
对B,在竖直方向上有:
mg-N′=may,
则:N′=mg-may=N=mgcos2θ.
答:(1)A对斜面的压力大小F=(m+M)gcosθ
(2)A对B的支持力大小N=mgcos2θ.
N=(m+M)gcosθ
则A对斜面的压力为:F=N=(m+M)gcosθ.
在斜面方向上有:(M+m)gsinθ=(M+m)a
解得:a=gsinθ.
(2)将加速度a分解为水平方向和竖直方向,有:
ay=gsinθ?sinθ=gsin2θ
对B,在竖直方向上有:
mg-N′=may,
则:N′=mg-may=N=mgcos2θ.
答:(1)A对斜面的压力大小F=(m+M)gcosθ
(2)A对B的支持力大小N=mgcos2θ.
点评:解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解,注意整体法和隔离法的运用.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
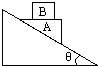 如图,在光滑的倾角为θ的固定斜面上放一个劈形的物体A,其上表面水平,质量为M.物体B质量为m,B放在A的上面,先用手固定住A.
如图,在光滑的倾角为θ的固定斜面上放一个劈形的物体A,其上表面水平,质量为M.物体B质量为m,B放在A的上面,先用手固定住A.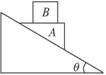
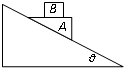 如图,在光滑的倾角为θ的固定斜面上放一个劈形的物体A,质量为M,其上表面水平且粗糙.质量为m的物体B放在A的上面,AB能保持相对静止并一起沿斜面下滑,求
如图,在光滑的倾角为θ的固定斜面上放一个劈形的物体A,质量为M,其上表面水平且粗糙.质量为m的物体B放在A的上面,AB能保持相对静止并一起沿斜面下滑,求