题目内容

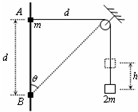（2013?怀远县模拟）如图所示，将质量为2m的重物悬挂在轻绳的一端，轻绳的另一端系一质量为m的环，环套在竖直固定的光滑直杆上，光滑定滑轮与直杆的距离为d．现将环从与定滑轮等高的A处由静止释放，当环沿直杆下滑距离也为d时（图中B处），下列说法正确的是（重力加速度为g）（　　）
分析：环刚开始释放时，重物的加速度为零，根据牛顿第二定律判断绳子的拉力大小．根据数学几何关系求出环到达B处时，重物上升的高度．对B的速度沿绳子方向和垂直于绳子方向分解，在沿绳子方向上的分速度等于重物的速度，从而求出环在B处速度与重物的速度之比．环和重物组成的系统，机械能守恒．
解答：解：A、环刚开始释放时，重物在瞬间加速度为零，则绳子的张力等于重物的重力，即T=2mg．故A正确．
B、环到达B时，绳子收缩的长度等于重物上升的高度，所以h=
2
d-d．故B正确．
C、对B的速度沿绳子方向和垂直于绳子方向分解，在沿绳子方向上的分速度等于重物的速度，有：vcos45°=v重物，所以
v
v重物
=
2
．故C错误．
D、环和重物组成的系统，只有重力做功，系统机械能守恒．故D错误．
故选AB．
点评：解决本题的关键知道系统机械能守恒，知道环沿绳子方向的分速度的等于重物的速度．
练习册系列答案
相关题目
（2013?怀远县模拟）测金属电阻率实验：
（1）测长度时，金属丝的起点、终点位置如图（a），则长度为：
60.50
60.50
cm；
（2）用螺旋测微器测金属丝直径，示数如图（b），则直径为：
1.981
1.981
mm；
（3）用多用表“Ω×1”挡估测其电阻，示数如图（c），则阻值为：
5
5
Ω；
（4）在图d中完成实物连线；
（5）闭合开关前应将滑动变阻器的滑片P移至最
左
左
（填“左”或“右”） 端．
（2013?怀远县模拟）某同学在做“利用单摆测重力加速度”的实验中，先测得摆线长为101.00cm，摆球直径为2.00cm，然后用秒表记录了单摆振动50次所用的时间为101.5s．则：
（1）他测得的重力加速度g=
9.76
9.76
m/s2．（计算结果取三位有效数字）
（2）他测得的g值偏小，可能原因是：
B
B

A．测摆线长时摆线拉得过紧．
B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了．
C．开始计时时，秒表过迟按下．
D．实验中误将49次全振动计为50次．
（3）为了提高实验精度，在实验中可改变几次摆长l并测出相应的周期T，从而得出一组对应的l和T的数值，再以l为横坐标、T2为纵坐标将所得数据连成直线，并求得该直线的斜率K．则重力加速度g=
4π2
K
4π2
K
．（用K表示）
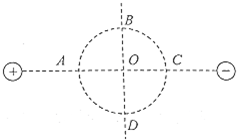（2013?怀远县模拟）如图所示，在等量异种电荷形成的电场中，以电荷连线中点O为圆心画一圆，交连线于A、C两点，交连线中垂线于B、D两点．下列说法中正确的是（　　）
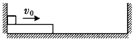（2013?怀远县模拟）如图所示，在光滑水平面上有一质量为M的长木板，长木板上有一质量为m的小物块，它与长木板间的动摩擦因数为μ．开始时，长木板与小物块均靠在与水平面垂直的固定挡板处，某时刻它们以共同的速度v0向右运动，当长木板与右边的固定竖直挡板碰撞后，其速度的大小不变、方向相反，以后每次的碰撞均如此．设左右挡板之间的距离足够长，且M＞m．
（1）要想物块不从长木板上落下，则长木板的长度L应满足什么条件？
（2）若上述条件满足，且M=2kg，m=1kg，v0=10m/s，求整个系统在第5次碰撞前损失的所有机械能．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网